Inscription / Connexion Nouveau Sujet
Travail et puissance
Bonjour j'aurai besoin d'aide sur la question 4)a) Voici l'énoncé:
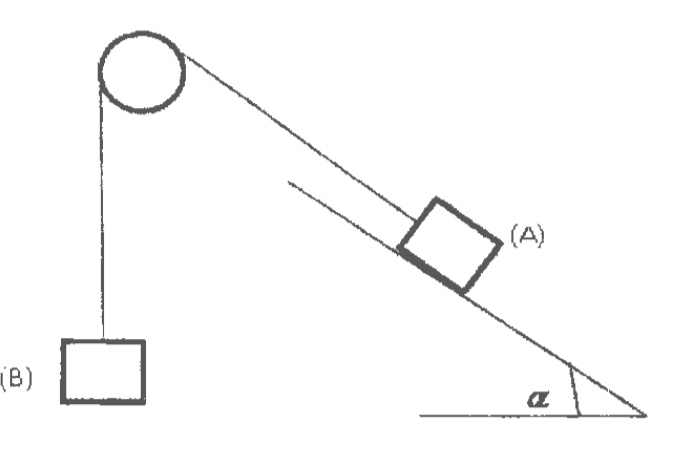
On considère un système attelé constitué de deux solides A et B, de masses respectives mA et mB, reliés par un fil inextensible de masse négligeable passant par la gorge d'une poulie de rayon r=10cm et de masse négligeable. Le solide A glisse sur un plan incliné lisse formant un angle a = 30° avec l'horizontal. (Voir figure)
1) Représenter toutes les forces qui s'exercent sur les solides A et B.
2) Calculer la valeur absolue des moments des forces qui s'exercent
sur la poulie. En déduire le sens de rotation de la poulie.
3) Pour une rotation d'un angle 0=3,2pi rad, calculer les travaux des
poids des solides (A) et(B).
4) Si la poulie continue à tourner, après un certain temps, le fil se détache du solide (A). En supposant que le solide (B) descend à vitesse constante, il s'exerce sur la poulie des forces de frottement qui
se traduisent par l'existence d'un couple de moment Mdelta(f)par rapport à l'axe de rotation (delta)passant par le centre de la poulie.
a) Calculer le moment de ce couple de frottement.
Bonjour,
Pourrais-tu commencer par mettre à jour ton profil (qui affiche seconde et non première) ?
extrait de 
la FAQ du forum :Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau topic ?
équivalences des systèmes de niveaux scolairesEnsuite, tu n'es pas nouveau, tu connais la règle :
moteur de recherche
page de choix du forum
fiches du siteQu'as-tu été en mesure de faire ?
Oui désolé j'ai représenté les forces pour les solides A et B
Pour le solide A : on a le poids PA, la réaction R, et la tension TA
Pour le solide B : on a le poids PB et la tension TB
2) pour cette question:
J'ai obtenu 4 forces à noter le poids de la poulie , la réaction de l'axe,et les deux tensions que j'ai noté T'A et T'B
On sait que M(R)=M(P)=0
M(T'A)=T'A *r
M(T'B)=-T'B*r
En faisant l'étude de chaque solide j'ai obtenu TA=mAgsina et comme c'est le meme fil T'A=TA=mAgsina
Et TB=mBg et comme c'est le meme fil T'B=TB=mBg
Donc |M(P)+M(R)+M(T'A)+M(T'B)|=
|0+0+mAgrsina-mBgr|=|-0,15|=0,15N.m
Donc la poulie tourne vers B
3)Calculons les travaux des poids des solides (A) et (B)
S=r*ø où ø=3,2pi rad
A.N:S=0,1*3,2pi=1m
W(Pb)=mBgS
A.N:W(Pb)=0,2*10*1=2J
W(Pa)=-mAg*hA où hA=Ssina
W(Pa)=-mAgSsina
A.N:W(Pa)=-0,1*10*1sin30
W(Pa)=-0,5J
4) je bloque sur cette question
Tu n'as toujours pas mis à jour ton profil, prends 2 min pour le faire
Oui désolé j'ai représenté les forces pour les solides A et B ce serait bien d'avoir le schéma
Pour le solide A : on a le poids PA, la réaction R, et la tension TA ok
Pour le solide B : on a le poids PB et la tension TB ok
2) pour cette question:
J'ai obtenu 4 forces à noter le poids de la poulie (non ! Relis l'énoncé) , la réaction de l'axe (non et je ne vois pas à quel force tu fais référence),et les deux tensions que j'ai noté T'A et T'B ok
On sait que M(R)=M(P)=0 non, cf. commentaires ci-dessus
|M(T'A)|=T'A *r ok
|M(T'B)|=|-T'B*r| = ... (l'énoncé te demandant une valeur absolue
En faisant l'étude de chaque solide j'ai obtenu TA=mAgsina tu n'expliques pas comment tu as trouvé cette relation
et comme c'est le meme fil T'A=TA=mAgsina non, ce n'est pas une notion de "même fil" mais de fil inextensible qui sert de justification
Et TB=mBg tu n'expliques pas comment tu as trouvé cette relation
et comme c'est le meme fil T'B=TB=mBg non, ce n'est pas une notion de "même fil" mais de fil inextensible qui sert de justificatio
Donc |M(P)+M(R)+M(T'A)+M(T'B)|=
|0+0+mAgrsina-mBgr|=|-0,15|=0,15N.m
Donc la poulie tourne vers B pourquoi donc ? Comment justifies-tu ça ?
3)Calculons les travaux des poids des solides (A) et (B)
S=r*ø où ø=3,2pi rad à quoi correspond ce "S" ?
A.N:S=0,1*3,2pi=1m
W(Pb)=mBgS explique ce que tu fais
A.N:W(Pb)=0,2*10*1=2J
W(Pa)=-mAg*hA où hA=Ssina idem ici, explique ce que tu fais
W(Pa)=-mAgSsina
A.N:W(Pa)=-0,1*10*1sin30
W(Pa)=-0,5J
4) je bloque sur cette question quels théorèmes as-tu vu pour les solides en rotation autour d'un axe (sachant que la vitesse est supposée constante => accélération = ?)
Annuler
connectez vous