Inscription / Connexion Nouveau Sujet
Travail du poids
Bonsoir à tous, j'ai un exo' pour demain, j'y ai réfléchi et je ne comprends pas du tout par où m'y prendre...
Un pendule est constitué d'une bille de centre C et de masse m= 100g reliée à un point fixe O par un fil inextensible de longueur l= 50cm et de masse négligeable. On note
la valeur de l'angle entre le fil et la verticale à un instant quelconque. On écarte le pendule de sa position d'équilibre d'un angle de valeur =o= 30° et on le lâche sans vitesse initiale.
a. Etablir l'expression littérale du travail du poids lorsque l'angle entrela verticale et le fil passe de la valeur
=o à une valeur appartenant à l'intervalle [-o ; o].
b. Calculer le travail du poids de la bille lorque la valeur
passe de o à 0.
c. Calculer le travail du poids de la bille lorsque la valeur
passe de o à -o.
d. Que peut-on dire du travail de la force exercée par le fil sur la bille ?
Donc si vous pouviez m'aider ce serait sympa
Bonsoir.
Je t'aide en te faisant la Qa)
Qa) Inspecte ce schéma (remplace 
par )
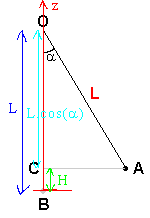
Tu peux donc exprimer le travail :
W() = m.g.(zA - zB) = mg.H = mg.{L - L.cos
} = mgL(1 - cos )
Qb) Effectue le calcul !
Qc) Sans calcul !
Si on passe de la position de (+0) à (-0), on remonte à l'altitude de départ... donc W = ?
Qd) Sans calcul !
Sur un temps très très court, quel est l'angle formé par le vecteur-force et un tout petit bout de déplacement/trajectoire
?
J'ai peut-être été trop rapide...
pour la Qa)
W = mg.(zinitiale - zfinale) = mg.(zA - zB)
Si on pose que zB = 0 (origine des altitudes au point le plus bas donc), alors W = mg.zA
Et zA = zC = H = L - L.cos(0)
D'où W = mgL.(1 - cos 0) lorsque l'on passe de 0 à 0
WAB (P→) = m . g . L (cos θ - cos θ0).
Oui, mais comme
= 0 (au final !), alors cos = 1, donc tu retombes sur la formule que je viens de t'écrire ! Ah, j'étais resté sur la question a)
Ok, alors tu as donc :
W = mgL.{cos(-0) - cos(+0)}
Et je te rappelle que cos(-x) = cos(x) par parité de la fonction cosinus, tu en déduis quoi ?
Nan mais c'est pas W = mgL.{cos(-0) - cos(+0)} car c'est un angle au hasard, pas forcement o
C'est donc W = mgL.{cos() - cos(+0)}
Ca, on est d'accord, j'avais très bien compris ce que tu voulais dire !
C'est la formule générale applicable à n'importe quel angle
(D'ailleurs, relis ton post de 19h41 )
Donc, si maintenant tu adaptes à ton exo :
Qa) = 0
Qb) = (-0)
Continue les calculs !
Annuler
connectez vous