Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Travail de forces

Posté par
Murdoch 15-03-20 à 15:39

Bonsoir, j'ai un exercice de physique à faire que je ne comprend pas. Pouvez-vous m'aider?

Énoncer - Questions  - Donnée - Réponses
.
.
.
Un tapis roulant de longueur l=AB=5,0m est utilisé pour charger des bagages dans la soute d'un avion. Le tapis est incliné d'un angle =15° par rapport à l'horizontale. Une valise de masse m=20kg, est entraînée par ce tapis avec une vitesse de valeur v constante.

Donnée : g=9,81N.kg-1

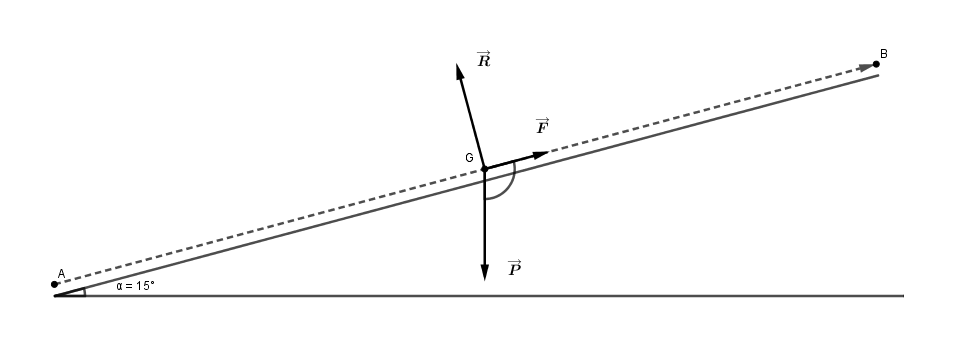
1. La valise est soumise à son poids \vec{P}, à l'action du tapis modélisée par une force motrice \vec{F} dans le plan du tapis et par une force \vec{R} perpendiculaire au plan du tapis. Schématiser ces forces.

---> Schéma fait : une droite AB horizontale représentant le tapis, une croix à la droite (AB) symbolisant la valise. un vecteur \vec{P} perpendiculaire au plan du tapis (AB) partant de la croix et allant vers le bas. Enfin, un vecteur  \vec{R} perpendiculaire au plan du tapis (AB) partant de la croix et allant vers le haut.

2a. Montrer que le travail de poids \vec{P} lors du déplacement de la position A à la position B est : W_{A\rightarrow B}(\vec{P})=-m\times g\times l\times sin(\alpha )

---> Je comprend tout car cela découle de la fonction :W_{A\rightarrow B}(\vec{P})=P\times AB\times cos(\vec{P}, \vec{AB})
avec P qui devient m*g avec un - devant car c'est un travail résistant.
AB qui devient l comme dit dans l'énoncer.

Mais je ne comprend pas comment cos(\vec{P}, \vec{AB}) devient sin(\alpha )

2b. Exprimer le travail des deux autres forces constantes

---> donc W_{A\rightarrow B}(\vec{F})=F\times l\times cos(\vec{F}, \vec{AB})
et W_{A\rightarrow B}(\vec{R})=R\times l\times cos(\vec{R}, \vec{AB})
mais je ne pense pas ça correcte.

3a. Justifier que l'énergie cinétique reste constante au cours de ce déplacement.

3b. Calculer la valeur de la force motrice \vec{F} exercée par le tapis sur la valise.
.
.
.
Merci d'avance🤗

Posté par
odbugt1re : Travail de forces 15-03-20 à 15:53

Bonjour,

Citation :
---> Schéma fait : une droite AB horizontale représentant le tapis, une croix à la droite (AB) symbolisant la valise. un vecteur \vec{P} perpendiculaire au plan du tapis (AB) partant de la croix et allant vers le bas. Enfin, un vecteur  \vec{R} perpendiculaire au plan du tapis (AB) partant de la croix et allant vers le haut.

A mon avis le segment AB n'est pas horizontal, mais il est incliné d'un angle par rapport à l'horizontale.


Plutôt que de décrire le schéma, pourquoi ne pas le scanner ou le photographier ?
Il serait alors plus simple de répondre à tes questions

Posté par
Murdochre : Travail de forces 15-03-20 à 16:04

Je n'y avait pas pensée, je viens de le refaire avec une inclinaison.

Travail de forces

Posté par
odbugt1re : Travail de forces 15-03-20 à 16:15

Ton schéma est à revoir.
En effet le réaction \vec{R} est perpendiculaire au plan du tapis donc perpendiculaire au segment AB

Posté par
Murdochre : Travail de forces 15-03-20 à 16:17

Il n'y a que cette erreur?

Posté par
odbugt1re : Travail de forces 15-03-20 à 16:26

Citation :
Il n'y a que cette erreur?

Pour le schéma : Oui, avec aussi (en haut et à droite) la direction du mouvement de la valise qui doit être inclinée et  pas horizontale.

Posté par
Murdochre : Travail de forces 15-03-20 à 16:31

D'accord donc ce schéma là est bon?
et pour la suite,

Posté par
Murdochre : Travail de forces 15-03-20 à 16:31

Murdoch @ 15-03-2020 à 16:31

D'accord donc ce schéma là est bon?
et pour la suite,


Travail de forces

Posté par
odbugt1re : Travail de forces 15-03-20 à 16:43

Question 2.a)
Tu écris que :   W_{A\rightarrow B}(\vec{P})=P\times AB\times cos(\vec{P}, \vec{AB})    ce qui est exact.

Tu devrais faire apparaître sur ta figure d'une part l'angle et d'autre part l'angle (\vec{P}, \vec{AB}) afin de constater que ce ne sont pas les mêmes.

Cela fait tu verras que cos(\vec{P}, \vec{AB})=-sin (\alpha)

Posté par
Murdochre : Travail de forces 15-03-20 à 16:47

moi je vois juste que cos (\vec{P}, \vec{AB}) = cos (90-\alpha )

Posté par
odbugt1re : Travail de forces 15-03-20 à 17:10

Regarde mieux :
L'angle (\vec{P}, \vec{AB}) n'est pas égal à (90 - ) mais à (90 + )
Or cos ((90 + )) = - sin ()

Travail de forces

Posté par
Murdochre : Travail de forces 15-03-20 à 17:16

J'était partie à l'inverse du sens du cercle trigonométrique ok je comprend mieux maintenant merci.
Mais par contre

odbugt1 @ 15-03-2020 à 17:10

Regarde mieux :
L'angle (\vec{P}, \vec{AB}) n'est pas égal à (90 - ) mais à (90 + )
Ok
Or cos ((90 + )) = - sin ()
Ce n'est pas ((90 + )) = + sin ()

Sinon ça ne confirme pas l'équation sur laquelle je doit retomber?

Posté par
odbugt1re : Travail de forces 15-03-20 à 17:33

Je ne connais pas ton niveau en formules trigonométriques, mais il est facile de vérifier avec une calculatrice que (par exemple) :
cos (90 + 15 ) = cos (105 ) = - 0,259
sin (15) = + 0,259
donc cos (90 + 15) = - sin (15)
C'est vérifiable pour n'importe quel angle autre que 15°
La relation est bien cos (90 + ) = - sin ()

Finalement :
W_{A\rightarrow B}(\vec{P})=P\times AB\times cos(\vec{P}, \vec{AB}) \\ P =mg \\ AB = L \\ cos(\vec{P}, \vec{AB} )= - sin (\alpha)
donne bien
W_{A\rightarrow B}(\vec{P})=-m~g~L~sin(\alpha )

Le travail du poids est négatif comme on pouvait s'y attendre .


Posté par
Murdochre : Travail de forces 15-03-20 à 17:40

À vrai dire en visualisant le cercle trigonométrique 105° on dépasse les \frac{\pi }{2} rad
Je n'y avait pas vraiment réfléchie très bien, maintenant j'ai compris merci.

Posté par
odbugt1re : Travail de forces 15-03-20 à 17:50

L'angle entre les vecteurs \vec P et \vec {AB} est l'angle dont il faut faire tourner (dans le sens trigonométrique) le vecteur \vec P pour l'amener sur le vecteur \vec {AB}

Ici sa valeur est en effet de 105°

Posté par
Murdochre : Travail de forces 15-03-20 à 18:08

Ma début de réponses pour la question 2b. est-elle correct?

Posté par
odbugt1re : Travail de forces 15-03-20 à 18:08

Remarque :

On peut amener le 1er vecteur sur le 2e en tournant dans un sens ou dans l'autre.
Cela change la valeur de l'angle, mais pas celle de son cosinus.

Posté par
odbugt1re : Travail de forces 15-03-20 à 18:10

Oui, tes réponses en 2b) sont bonnes, il reste à évaluer correctement les angles concernés.

Posté par
Murdochre : Travail de forces 15-03-20 à 18:22

Pour \vec{F}:

W_{A\rightarrow B}(\vec{F})=F\times AB\times cos(\vec{F},\vec{AB})
cos(\vec{F},\vec{AB}) = cos (0) =1
W_{A\rightarrow B}(\vec{F})=F\times l\times 1 = F\times l

Pour \vec{R}:

W_{A\rightarrow B}(\vec{R})=F\times AB\times cos(\vec{R},\vec{AB})
cos(\vec{R},\vec{AB}) = cos (90) =0
W_{A\rightarrow B}(\vec{R})= 0
.
Est-ce correct?

Posté par
odbugt1re : Travail de forces 15-03-20 à 18:44

Tout à fait correct.

Posté par
Murdochre : Travail de forces 15-03-20 à 18:47

3a. L'énergie cinétique reste constante au cours du déplacement car le tapis a une vitesse de valeur v constante.
.
Est-ce correct?

Posté par
odbugt1re : Travail de forces 15-03-20 à 18:50

Oui, c'est bon.

Posté par
Murdochre : Travail de forces 15-03-20 à 18:50

Je n'ai pas besoin de justifier autrement?

Posté par
odbugt1re : Travail de forces 15-03-20 à 18:59

v = cte
m = cte
donc Ec = (1/2)*m*v² = cte

Posté par
Murdochre : Travail de forces 15-03-20 à 19:02

D'accord par contre je ne comprend pas la dernière question, je ne vois pas comment faire

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:04

Il suffit d'appliquer le théorème de l'énergie cinétique sur le déplacement AB

Posté par
Murdochre : Travail de forces 15-03-20 à 19:07

Soit \Delta Ec = \Sigma W_{AB}(\vec{F})
donc \Delta Ec = W_{AB}(\vec{F}) + W_{AB}(\vec{P}) + W_{AB}(\vec{R}) =W_{AB}(\vec{F}) + W_{AB}(\vec{P})

Comme ça?

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:10

Oui.

Posté par
Murdochre : Travail de forces 15-03-20 à 19:23

Je ne suis quasiment sûr que mon résultat est incorrect :

\Delta Ec = W_{AB}(\vec{F}) + W_{AB}(\vec{P}) + W_{AB}(\vec{R}) =W_{AB}(\vec{F}) + W_{AB}(\vec{P})

W_{AB}(\vec{F}) = \Delta Ec - W_{AB}(\vec{P}) - W_{AB}(\vec{R})

F\times l = \frac{1}{2}mv^{2} + mg\times l\times sin (15) - 0

F = \frac{\frac{1}{2}mv^{2} + mg\times l\times sin (15) - 0}{l} = \frac{1}{2}mv^{2} + mg\times sin (15) - 0 = 0,5 \times 20 v^{2}+20\times 9,81\times sin (15)

F = 61 v^{2}

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:30

Incorrect en effet !

Quand tu écris : \Delta Ec = \Sigma W_{AB}(\vec{F})
Qu'est ce que \Delta Ec ~?

Posté par
Murdochre : Travail de forces 15-03-20 à 19:31

C'est l'énergie cinétique

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:41

Pas tout à fait !
Ec est l'énergie cinétique.
Mais Ec est ................

Posté par
Murdochre : Travail de forces 15-03-20 à 19:43

c'est la variation de l'énergie cinétique? Ça permet de faire le lien entre forces et variations de la vitesse

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:47

Absolument !
Et quelle est la valeur numérique ici dans le cas du trajet AB ?

Posté par
Murdochre : Travail de forces 15-03-20 à 19:48

AB est égal à 5m

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:48

Pardon ... faute de frappe !

Et quelle est sa valeur numérique ici dans le cas du trajet AB ?

Posté par
Murdochre : Travail de forces 15-03-20 à 19:49

C'est une constante

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:50

Je ne m'intéresse pas à la valeur de AB mais à la valeur de la variation de l'énergie cinétique de la valise entre A et B

Posté par
odbugt1re : Travail de forces 15-03-20 à 19:51

Oui, l'énergie cinétique est constante.
Donc que vaut sa variation ?

Posté par
Murdochre : Travail de forces 15-03-20 à 19:52

Elle est nulle ?

Posté par
odbugt1re : Travail de forces 15-03-20 à 20:03

Bien sûr !
Donc ....

Posté par
Murdochre : Travail de forces 15-03-20 à 20:05

Donc on résout comme si c'était W_{AB}(\vec{F}) + W_{AB}(\vec{P}) + W_{AB}(\vec{R}) = 0

Posté par
odbugt1re : Travail de forces 15-03-20 à 20:12

Oui.
Le conditionnel " si c'était " est maladroit
La variation d'énergie cinétique est égale à la somme des travaux des forces appliquées.

Posté par
Murdochre : Travail de forces 15-03-20 à 20:18

Donc cela nous donne :
W_{AB}(\vec{F}) + W_{AB}(\vec{P}) + W_{AB}(\vec{R}) = 0

W_{AB}(\vec{F}) = - W_{AB}(\vec{P}) - W_{AB}(\vec{R})

F\times l = m\times g\times l \times sin (15)-0

F= \frac{m\times g\times l \times sin (15)-0 }{l} = m\times g\times sin (15)

F = 20\times 9,81\times sin (15) = 51 N
.
Est-ce correct?

Posté par
odbugt1re : Travail de forces 15-03-20 à 20:22

Tout ce qu'il y a de plus correct.

Attention donc de ne plus confondre Energie cinétique et variation d'énergie cinétique !

Posté par
Murdochre : Travail de forces 15-03-20 à 20:24

Et bien on apprend de nos erreurs.
Je te remercie odbugt1 pour ton aide et ta patience. Bonne fin de soirée, et de week-end 🤗


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !