Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. SecondeForum de secondes PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau seconde
Partager :

Travail d'une force electrostatique

Posté par
fatogoma 17-12-15 à 17:03

bonjour j'ai besoin d'aide urgent pour l'execice suivant:
Dans une region de l'espace,regne un champ electrique uniforme d'intensit¡§0?7 E=1000v/m.
Dans le repere orthonorm¡§0?7(O,i,j,k) ce champ a pour expression E(vecteur)=Ei(vecteur).
Calculer le travail de la force electrostatique qui s'exerce sur un noyau d'helium(he010¡­5¡§C) lorsque cette particule passe du point A(2,0,0) au point B(4,2,0). l'unit¡§0?7 de longueur est le cm e= 1,6.10¡§C0106¥919C, q=2e.

***Niveau mis en accord avec ton profil***

Posté par
picardre : travail d'une force electrostatique 17-12-15 à 17:29

Bonjour.

Votre message est difficile à comprendre, beaucoup de caractères y sont illisibles.

On peut quand même vous fournir quelques pistes.

Exprimez vectoriellement, la force électrostatique \vec{F} qui s'exerce sur le noyau d'hélium dans le champ électrique \vec{E}

Cette force est-elle constante ou non ?

Quelle est l'expression du travail, W(\vec{F})_{A \rightarrow B}, d'une force constante \vec{F} lors d'un déplacement \vec{AB} ?

Quelles sont, dans le repère choisi, les coordonnées du vecteur \vec{AB} ?

Enfin un rappel de mathématiques : le produit scalaire de deux vecteurs \vec{u} et  \vec{v}, de coordonnées respectives (X, Y, Z) et (X', Y', Z') est :     \vec{u}.\vec{v} = XX' + YY' + ZZ'.

Avec tout ça, vous devriez pouvoir avancer.

A plus.

Posté par
fatogomare : travail d'une force electrostatique 17-12-15 à 19:12

merci.pou etre clair.
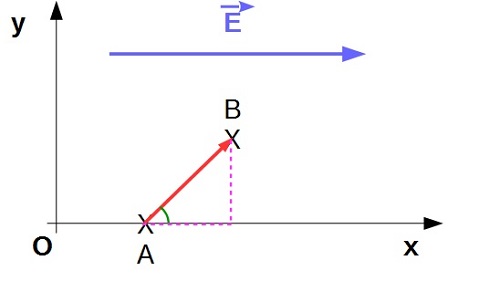
je voulais savoir comment placer le vecteur champ et  les points dans le repere?et comment calculer le travail dans le repere considere?

Posté par
picardre : Travail d'une force electrostatique 18-12-15 à 14:17

Citation :
je voulais savoir comment placer le vecteur champ et  les points dans le repere?
Je ne suis pas sûr qu'une figure soit ici d'un grand secours, mais si vous y tenez...
Comme toutes les coordonnées selon l'axe \vec{Oz}, de vecteur unitaire \vec{k}, sont nulles, vous pouvez faire un schéma dans le plan (xOy) muni du repère (O, \vec{i} , \vec{j}),

Si j'arrive à déchiffrer correctement votre énoncé, on a : \vec{E} = E  \vec{i} avec E = 1000 V.m-1.
Comment le vecteur \vec{E} est-il disposé par rapport au vecteur unitaire \vec{i} du repère ?

Quant aux points A et B, vous avez leurs coordonnées, il n'y a pas de difficulté à les placer dans le repère.

Citation :
comment calculer le travail dans le repere considere?
Relisez donc mon premier message.

A vous.

Posté par
fatogomare : Travail d'une force electrostatique 18-12-15 à 14:40

Le champ est uniforme donc je pense que la force est constante.
l'expression du travail est W(vecteur)=F(vecteur)¡ÁAB(vecteur) et en module W=F*AB*cos(F,AB).comment utiliser cette expression dans le repere?Si vous pouvez m'aider avec un schema 0Š4a serait plus comprehensive.

Posté par
picardre : Travail d'une force electrostatique 18-12-15 à 18:20

Citation :
Le champ est uniforme donc je pense que la force est constante.
Oui, c'est bien cela ; citez, pour justifier votre affirmation, la relation liant \vec{F} et \vec{E}.

Citation :
l'expression du travail est W(vecteur)=F(vecteur).AB(vecteur)
Correct aussi, mais le travail n'est PAS une grandeur vectorielle, c'est un nombre (on dit aussi, une grandeur scalaire).

Citation :
W=F*AB*cos(F,AB)
Exact aussi, mais plus long à utiliser dans le contexte de l'exercice, on ne connait ni AB, ni l'angle (\vec{F}, \vec{AB}).
Cette méthode peut néanmoins être utilisée, mais je vous en avais suggéré une autre utilisant les coordonnées des vecteurs qu'il est facile d'obtenir à partir des données fournies.

Citation :
Si vous pouvez m'aider avec un schéma
Qu'est-ce qui vous empêche de le faire seul ? Placer 2 points et un vecteur dont on connait les coordonnées, c'est du niveau d'une classe de 4° ou de 3°.
De plus, je continue de penser que ce schéma ne présente pas d'intérêt pour calculer le travail de la force électrique.

Posté par
fatogomare : Travail d'une force electrostatique 18-12-15 à 19:08

merci.montrer moi alors votre methode.

Posté par
picardre : Travail d'une force electrostatique 18-12-15 à 19:17

Regardez donc le rappel mathématique du message que je vous ai envoyé la 17/12 à 17 h 29

Posté par
fatogomare : Travail d'une force electrostatique 18-12-15 à 19:29

ok.le probleme est que nous avons vue une leçon de math sur le vecteur de l'espace.donc si vous pouvez faire l'application numerique pour que je puisse comprendre.

Posté par
picardre : Travail d'une force electrostatique 19-12-15 à 14:29

Citation :
si vous pouvez faire l'application numerique pour que je puisse comprendre.
Autrement dit, vous me demandez de faire l'exercice à votre place ; je vous ai donné tous les éléments nécessaires, recopier un corrigé ne vous fera guère progresser.

1° méthode : en utilisant les coordonnées.

\vec{E} = 10^3 \vec{i}  +  0 \vec{j}  +  0 \vec{k}

\vec{F} = q \vec{E}   avec q = 2 e = 3.2 \times 10^{-19} C

Soit :   \vec{F} = 3.2 \times 10^{-19} (10^3 \vec{i}  +  0 \vec{j}  +  0 \vec{k})

ou :   \vec{F} = ( 3.2 \times 10^{-16} \vec{i}  +  0 \vec{j}  +  0 \vec{k})

Les coordonnées de  \vec{F} sont donc (en N)  (F_x = 3.2 \times 10^{-16}  ;  F_y = 0  ;  F_z =0)

Coordonnées de A (en m)   (x_A = 2 \times 10^{-2}  ;  y_A = 0  ;  z_A = 0 )

Coordonnées de B (en m)   (x_B = 4 \times 10^{-2}  ;  y_B= 2 \times 10^{-2}  ;  z_B = 0 )

Coordonnées de \vec{AB}  :   (X_{AB} = (x_B - x_A)  ;  Y_{AB} = (y_B - y_A)  ;  Z_{AB} = (z_B - z_A))

Soit (en m)    \vec{AB}  :  ( 2 \times 10^{-2}   ;   2 \times 10^{-2}  ;  0)


Le travail de la force électrostatique est donné par : W = \vec{F} . \vec{AB}  ,  c'est à dire encore :  W = (F_x . X_{AB})  +  (F_y . Y_{AB})  +  (F_z . Z_{AB})

Numériquement : W = (3.2 \times 10^{-16}  \times  2 \times 10^{-2})  +  (0 \times  2 \times 10^{-2}) +  (0  \times  0)
C'est à dire, finalement : W = 6.4 \times 10^{-18} J

2° méthode en utilisant : W = \vec{F} . \vec{AB} = F . AB . cos ( \vec{F}, \vec{AB})

Valeur de F (voir 1° méthode) : F = 3.2 \times 10^{-16}  N

Valeur de AB (voir 1° méthode) : AB = \sqrt{{X_{AB}}^2 + {Y_{AB}}^2 +{Z_{AB}}^2}
Soit :  AB = \sqrt{{(2\times10^{-2}})^2 + {(2\times10^{-2}})^2 + 0}
C'est à dire  AB = 2.83 \times 10^{-2}  m

Calcul de  cos ( \vec{F}, \vec{AB}) (cf schéma ci-dessous)

cos ( \vec{F}, \vec{AB})= \dfrac{Y_{AB}}{AB}
Soit :  cos ( \vec{F}, \vec{AB})= \dfrac{2\times10^{-2}}{2.83 \times 10^{-2} } = 0.707

Finalement, comme :   W = \vec{F} . \vec{AB} = F . AB . cos ( \vec{F}, \vec{AB})
on obtient numériquement : W = 3.2 \times 10^{-16} \times 2.83 \times 10^{-2} \times 0.707 = 6.4 \times 10^{-18} J



Je n'ai rien vérifié, mais j'estime avoir bien travaillé, et vous ?

Au revoir.

Travail d\'une force electrostatique


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !