Inscription / Connexion Nouveau Sujet
Travail d'une force
Bonjour,
j'aimerais que vous m'aider à traiter cet exercice dont l'énoncé est:
Valentin veut déplacer un réfrigerateur de 170Kg. Il développe une force motrice F de module 1250N par l'intermediaire d'une ficelle inclinée de alpha=30° par rapport à l'horizontale. La vitesse de déplacement est constante sur 13 m. Le sol est horizontal et recouvert d'une moquette.
1)Calculer les travaux du poids et de la force motrice.
2)Après avoir précisé le principe utilisé, determiner le travail de la réaction, puis son intensité. on suppose que ce vecteur est incliné de 45° sur l'horizontale.
3) Deduire l'intensité des forces de frottement supposées constante.
4)Calculer la puissance developpée par Valentin si V=0,5m/s.
on donne cos30°=0,86 ; g=10N/Kg.
Ma piste.
1)Le travail du poids;
W(P)=mgh or h=0 dans ce cas(pas d'altitude), donc W(P)=0 J.
le travail de F est égal au produit scalaire du vecteur force (F) et le vecteur AB(distance: si l'on admet qu'on déplace le réfrigerateur d'un point A vers un point B).
Ainsi W(F)=F*AB*cos30°=13975 J.
2) Application du theorême de l'énergie cinétique.
ΔEC=Ec(final)-Ec(initial)=W(P)+W(R)+W(F).
or ΔEc=0 car la vitesse est constante.
Ainsi W(R)=-W(F)=-13975 J.
W(R)=R*AB*cos45° => R=W(R)/(AB*cos45°)=-1520,27 N Donc le module de la réaction est de 1520,27 N.
3) Intensité de f
(j'en sais vraiment pas comment trouver f)
4)Puissance developpée:
P=W(F)/t => P=13975/26=537,5 W.
Bonjour,
Question 3 :
La réaction qui est inclinée de 45° par rapport à l'horizontale peut être décomposée en deux forces :
L'une verticale, donc perpendiculaire au déplacement, ne travaille pas.
L'autre, horizontale et de sens opposé à la vitesse, n'est rien d'autre que la force de frottement dont tu cherches l'intensité.
L'équilibre se traduit par :
R+F+P=0 (en vecteur)
or R=Rn+f(en vecteur)
=> Rn+f+F+P=0( en vecteur )
en projetant sur l'axe xx' on a :
-f+Fx=0 => f=Fx or Fx=F*cos30°
=> f=F*cos30°=0,86*1250=1075 N ?
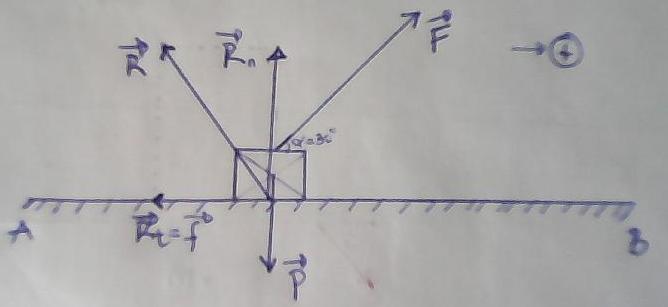
L'équilibre se traduit par :
C'est exact en dépit d'une grosse maladresse au début.
Tu parles d'équilibre là ou en réalité il existe un mouvement à vitesse constante ( voir énoncé )



