Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Traction d'une caravane

Posté par
Jeje34 07-02-09 à 12:59

Bonjour,
Je compte sur votre aide, il me manque plein de réponses.

Citation :
Une voiture de masse M = 1000 kg tracte une caravane de masse m = 650 kg à vitesse constante v = 70 km/h sur une reoutr rectiligne. La force de traction exercé par la voiture sur la caravane a pour valeur F = 200N.

1) On considère le système {caravane}. En admettant que le sol et l'air exercent sur le système une force f constante unique, qui s'oppose a son déplacement. Représenter sur un schéma toutes les forces qui s'exercent sur le système.
2) Quelle relation vectorielle existe t'il entre ces forces ? Justifier.
3) Déterminer la valeur de f.
4) Quelles sont les forces qui effectuent un travail moteur, résistant ou nul ?
5) Calculer le travail de chacune des forces pour un déplacement durant 10 s.
6) Calculer la somme des travaux des forces s'exercant sur le déplacement envisagé. Le résultat était-il prévisible ? Justifiez.


1)
Les forces exercées sur le système peuvent être modélisées par :
- action de la Terre : le poids P
- action de la voiture : Fvoiture/caravance
- action de soutien du sol : Rn
- action de frottements : f

2) Le centre d'inertie du système a un mouvement rectiligne uniforme (v=70km/h), il vérifie le principe d'inertie donc : P + Fvoiture/caravance + Rn + f = O (vecteur nul)

3) ?

4)
P et Rn : nul
f : résistant
Fvoiture/caravance : moteur
(Comment justifier ?)

5)
distance parcourue en 10 secondes, on sait que V (km/h) = d (km) / t (h), on a :
10 s = 2,78 x 10-3 h
d = v x t = 70 x 2,78 x 10-3 = 1,97 x 10-1 km

???


6) ???

Posté par
Marc35re : Traction d'une caravane 07-02-09 à 18:39

Bonjour,
D'après le texte, la réaction due à la route et la force de frottements ne forment qu'une seule force f.
- le poids P normal au sol et dirigé vers le bas
- la force de traction F de la voiture parallèle au sol et dirigé dans le sens du déplacement.
- réaction de la route + frottements f : force dirigée vers le haut mais inclinée vers l'arrière

2) \vec{P}\,+\,\vec{T}\,+\,\vec{f}\,=\,\vec{0}
justifié par la 1ère loi de Newton, la vitesse étant constante.

3) Il suffit d'écrire :
\vec{P}\,+\,\vec{T}\,+\,\vec{f}\,=\,\vec{0}\vec{f}\,=\,\vec{P}\,+\,\vec{T}
Les vecteurs \vec{f}  et  \vec{P}\,+\,\vec{T}  sont opposés puisque leur somme est nulle.
Donc : |\vec{f}|\,=\,|\vec{P}\,+\,\vec{T}|

4)
travail moteur => F parce qu'elle a même sens que le déplacement.
travail résistant => la composante de f parallèle à la route
travail nul => le poids et la composante de f normale à la route parce que ces forces ont une direction normale au déplacement.

On voit si tu comprends ça et on continue ensuite...

Posté par
Jeje34re : Traction d'une caravane 08-02-09 à 13:12

Bonjour Marc, merci pour ton aide.
Donc pour le 1), j'ai compris j'ai donc combiné Rn et f.
Pour le 2) pareil, le principe d'inertie est toujours vérifié.
Pour le 3), j'ai jamais su ce que signifié les normes, si tu peux m'éclairer.


1)
Les forces exercées sur le système peuvent être modélisées par :
- action de la Terre : le poids P (vertical, vers le bas)
- action de la voiture : Fvoiture/caravance (horizontal, dans le sens du déplacement)
- action de soutien du sol et des frottements : Rn (vers le haut, incliné a 45° vers l'arrière)

2) Le centre d'inertie du système a un mouvement rectiligne uniforme (v=70km/h), il vérifie le principe d'inertie donc : P + Fvoiture/caravance + f = O (vecteur nul)

3)
P+ Fvoiture/car. + f  = 0 <==> f = P + Fvoiture.car.
Les vecteurs f et P + Fvoiture  sont opposés puisque leur somme est nulle.
Donc : |f| = |P+Fvoiture|

4)
P : nul
f : résistant
Fvoiture/caravance : moteur

Merci !

Posté par
Marc35re : Traction d'une caravane 08-02-09 à 20:24

La norme d'un vecteur, c'est sa longueur.
Un vecteur est défini par 3 choses :
- sa direction
- son sens
- sa norme (autrement dit, la longueur du segment qui porte le vecteur)

As-tu besoin d'autre chose ?

Posté par
Jeje34re : Traction d'une caravane 08-02-09 à 20:56

Merci !

Mais comment je peux trouver un chiffre numérique pour représenté f ?
Y'a une formule ?

Je dois calculer le travail de chacune des forces ?

Posté par
Jeje34re : Traction d'une caravane 08-02-09 à 21:23

Autre question :
Le point d'application de f se trouve ou ?

Posté par
Marc35re : Traction d'une caravane 08-02-09 à 21:28

La masse totale à tracter est m = 1000+650 = 1650 kg
Le poids correspondant est P = 1650 x 9,81  N
P = 16186,5 N
La force de traction est T = 200 N.
Ces deux forces étant perpendiculaires, il est facile de calculer la norme de la somme |\vec{P}\,+\,\vec{T}|  par le théorème de Pythagore.
|\vec{P}\,+\,\vec{T}|\,=\,\sqrt{|\vec{P}|^2\,+\,|\vec{T}|^2}\,=\,sqrt{16186,5^2\,+\,200^2}
Et, comme nous l'avons vu, \vec{f}\,=\,\vec{P}\,+\,\vec{T} |\vec{f}|\,=\,|\vec{P}\,+\,\vec{T}|
Donc  |\vec{f}|\,=\,sqrt{16186,5^2\,+\,200^2}

sauf erreur éventuelle...

Posté par
Marc35re : Traction d'une caravane 08-02-09 à 21:29

Si on fait le bilan, quelles questions reste-il ?

Posté par
Marc35re : Traction d'une caravane 08-02-09 à 21:32

Toutes les forces ont pour point d'application  le centre d'inertie...

Posté par
Jeje34re : Traction d'une caravane 08-02-09 à 21:38

Le centre d'inertie = Le centre de gravité de la caravane ?

Sinon la norme est en quelle unité ?

Merci pour l'aide.

Posté par
Marc35re : Traction d'une caravane 09-02-09 à 10:41

"Le centre d'inertie = Le centre de gravité de la caravane ?"
le centre de gravité de l'ensemble voiture-caravane.
La norme d'une force est en Newton, bien sûr...
C'est la norme qui indique l'amplitude d'une force, le "reste" du vecteur indique sa direction et son sens (et son point d'application aussi).

Cet exercice n'est pas très difficile et tous les exercices de ce genre se résolvent de la même façon à quelques variantes près.
Là, on met en un seul vecteur la réaction du support, qui est verticale et vers le haut, et la force de frottement, qui peut se représenter par une force parallèle à la route et vers l'arrière. Quand on fait la somme vectorielle des deux, on a un vecteur vers le haut et incliné vers l'arrière.

Posté par
Jeje34re : Traction d'une caravane 09-02-09 à 10:59

Ah mais en fait norme = valeur, c'est compris.

Par contre il me reste la question 5, je ne sais pas quelle formule utilisé.

Pour le poids : WAB(P) = M g (Za - Zb) ?

Posté par
Marc35re : Traction d'une caravane 09-02-09 à 11:33

Pour le travail du poids, c'est simple WP = 0 parce qu'il est normal au déplacement.
Pour la force de traction, le travail est positif parce que la force est dans le sens du déplacement. Mais il faut calculer la longueur parcourue pendant 10 s.
La vitesse étant de 70 km.h-1, 7.104/3600 19,44 m.s-1. d = vt d = (7.104/3600) 10 = 194,44 m.
WF = F d = 200.(7.104/3600) 10 = 38,88.103 J
(le nombre de chiffres significatifs est arbitraire)
Pour f, c'est un peu compliqué. Il faut la décomposer sur la verticale à la route et sur la parallèle à la route. La composante sur la verticale ne travaille pas (normale au déplacement). Seule la composante parallèle à la route travaille mais il faut la calculer. Et, pour cela, il faut calculer l'angle entre f et la route.
Il faut que je fasse un schéma pour que ce soit plus clair...

Posté par
Jeje34re : Traction d'une caravane 09-02-09 à 11:50

Dans le calcul, que représente le 10 ?

En tout cas merci beaucoup !

Posté par
Marc35re : Traction d'une caravane 09-02-09 à 12:32

Le 10, c'est le temps 10 s.
Voilà le schéma :
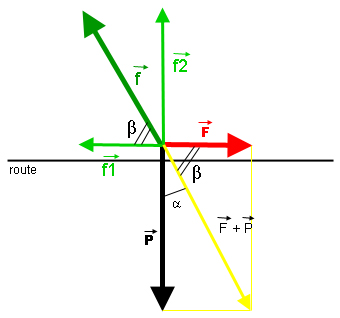
Traction d\'une caravane

\vec{f1}  est la partie de  \vec{f}  qui travaille.
f1 = f cos
Et tan = P / F
Donc  Wf1 = -f1 d
On a - parce que le travail est résistant, f1 étant en sens opposé au déplacement

Posté par
Marc35re : Traction d'une caravane 09-02-09 à 13:29

Tu dois trouver la somme des travaux égale à  0.
Pour le calcul de f1, ne fais pas d'approximation parce que l'angle est voisin de 90°. Donc la tangente et tan-1 varient très vite : il faut mettre la valeur exacte pour le calcul.
C'était prévisible parce que la vitesse étant constante, Ec = 0 et Ec = W   donc W = 0

|\vec{F}\,+\,\vec{P}|\,=\,\frac{|\vec{F}|}{cos\beta}
|\vec{f_1}|\,=\,|\vec{f}|\,cos\beta\,=\,|\vec{F}\,+\,\vec{P}|\,cos\beta\,=\,\frac{|\vec{F}|}{cos\beta}\,cos\beta\,=\,|\vec{F}|
W_F\,=\,|\vec{F}|\,d
W_f_1\,=\,-|\vec{f_1}|\,d
Comme   |\vec{f_1}|\,=\,|\vec{F}| W_F\,+\,W_f_1\,=\,0

Posté par
Jeje34re : Traction d'une caravane 09-02-09 à 13:52

Merci beaucoup je pense pouvoir me débrouiller avec ca !

Posté par
as6re : Traction d'une caravane 24-11-16 à 20:26

nnnnnnnnn

Posté par
Babe27re : Traction d'une caravane 04-05-17 à 16:03

Bonjour . Après avoir perdu l'énoncé de mon DM contenant des exercices dont celui-ci , je voudrais savoir où se trouve ce exercice ? dans quel livre ? . S'il vous plait


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !