Inscription / Connexion Nouveau Sujet
Tension divisée
Bonjour,
On considère le circuit suivant :
1. Exprimer U1 et U2 en fonction de E.
2. On règle E = 9V calculer les valeurs de U1 et U2.
Merci d'avance pour votre aide à cette exercice afin que je puisse comprendre et le faire.
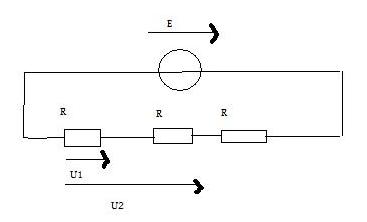
Dis moi, les résistances sont toutes identiques ?
Pour un conducteur Ohmique, on a UR = R.I. Les Conducteurs Ohmiques sont identiques, donc R est le même, donc la tension se répartie de manière égale aux bornes des 3 résistances...
Ça t'aide ?
Cela ne m'aide pas vraiment (mais néanmoins l'intensité on ne le connaît pas mais je crois qu'on suppose que les 3 résistances sont identiques).
Mais ce que je voudrais savoir c'est comment exprimer U1 et U2 en fonction de E.
Sachant que la loi que je sais est qui me permet de trouver une tension c'est la loi des mailles.
Et quand je l'applique à cette exercice cela me fait :
E-U2-U1=0
Ainsi on a : U2=E-U1
U1=E-U2
Donc quand je règle E = 9V, sachant que les trois résistances sont identiques, on a:
U2 = 9-3 = 6V ET U1 = 9-6 = 3V
C'est ce raisonnement que j'ai fait mais je ne suis pas sûr car le titre de l'exercice c'est "tension divisée".
Vérifier si mon raisonnement est juste et répondez moi le plus vite possible s'il vous plaît.
Merci d'avance pour vos aides.


