Bonjour,

1) Tu appliques la 2e loi de Newton au véhicule 1. Tu obtiens une relation (1)
2)Tu appliques la 2e loi de Newton au véhicule 2. Tu obtiens une relation (2)
3) Tu résous le système d'équation (1) et (2)

Remarque: L'énoncé n'évoque pas clairement la masse de la corde.  La méthode que j'ai exposée suppose qu'elle peut être négligée devant la masse des véhicules.

Pour le premier véhicule j'ai donc :

F ext =ma
Vu que les forces qui s'appliquent au véhicule sont le poids et la force qu'on apporte à la corde.
P + F = ma
m * g + F =ma
Mon raisonnement est-il juste ?

Bonsoir,

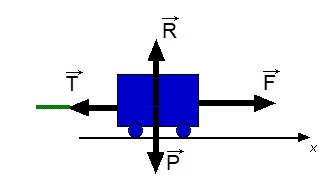
Tu as "zappé" la moitié des forces qui s'exercent sur le véhicule "bleu" :
Il y a en tout (si on néglige les frottements divers et variés) 4 forces :
La force motrice ,
Le poids du véhicule,
La réaction du sol,
La tension de la corde.

C'est (d'après la 2ème loi de Newton) la somme vectorielle de ces quatre forces qui est égale à m₂

Mais du coup on prend en compte uniquement le poids et la force motrice ?

Cette relation est-elle correcte pour le véhicule rouge ?
m * g + F =ma

Non.
La méthode, très classique est la suivante :
a) On choisit le système étudié : Ici le véhicule "bleu"
b) On choisit un référentiel adapté muni d'un repère Ox,Oy : Ici ce sera un référentiel terrestre. L'axe Ox est déjà sur la figure, l'axe Oy moins utile dans cet exercice est perpendiculaire à Ox et dirigé vers le haut.
c) On recherche toutes les forces extérieures non négligeables qui s'exercent sur le système étudié, sans en oublier, sans en inventer. En pratique, tout ce qui est en contact avec le système exerce une force extérieure et si le système se trouve sur la Terre, son poids est aussi une force extérieure à prendre en compte.
Pour chacune de ces forces on rassemble le maximum de renseignements possibles (direction, sens, valeur ...)
Ici quatre forces interviennent. Elles sont toutes à prendre en compte.
1)La force motrice ,
2)Le poids du véhicule,
3)La réaction du sol,
4)La tension de la corde.

d) On applique la 2ème loi de Newton :

On obtient une relation vectorielle qu'il va falloir transformer en relation algébrique.
Pour cela :

e) On fait deux projections de cette relation vectorielle sur les axex choisis :
Ici sur l'axe Ox : F + 0 - T + 0 = m₂.a donc F - T = m₂.a
Sur l'axe Oy : 0 - P + 0 + R = 0 donc P = R

C'est terminé pour le véhicule "bleu"
Si le problème n'a pas d'autres questions que le calcul de T, il est vrai que la projection sur l'axe Oy ne servira pas et donc que les forces n'interviendront pas. Ce n'est pas une raison pour les écarter d'emblée.

Il te faut recommencer tout cela pour l'autre véhicule.
Tu obtiendras de nouveau 2 relations (dont une seule vraiment utile)

En combinant les relations obtenues pour chaque véhicule tu obtiendras un système de deux équations à deux inconnues ( T et a ) et tu pourras donc répondre  à la question posée en éliminant a entre les deux relations.

a)Le système étudié est le véhicule rouge.
b)Référentiel:  terrestre
c)Forces intervenants :
   1)Poids du système
   2)Tension de la corde
   3)Réaction du sol
   4)Force motrice

d)P + T + R + F = m1 * a

Jusque là est ce correct ?

Cette force permet de faire avancer le véhicule bleu?
Du coup ne permet-elle pas de faire aussi avancer le véhicule rouge ?

Bonjour,

J'ai compris vos explications.
Donc pour le véhicule rouge j'ai donc:

P + T +R = m₁a
Ox : 0 + T + 0 = m₁a   R = P

J'ai donc T = m₁a
et T= F -(m₂a)

Je dois supprimer a juste en utilisant ces deux relations ?

Bonjour,

Bonjour,  excusez moi pour l'attente.

J'en arrive donc à ça :
T/ m₁ = (F - T) / m₂

et donc j'en arrive à :
T = (F * m₁) / (m₂ + m₁)

Est ce juste ?

Je pense avoir compris la méthode, je reposterai peut être si j'ai encore des problèmes, mais merci à vous pour votre aide et vos explications, elles étaient très claires et encore désolé pour le retard.

Oui, c'est exact.

Remarque :
On aurait pu aussi choisir, en premier lieu, pour système l'ensemble (Véhicule bleu + corde + Véhicule rouge)
Les forces extérieures sont alors:



et la 2e loi de Newton s'écrit :



La projection de cette relation sur Ox est :
F = (m1 + m2) a



On considère ensuite comme système soit le véhicule rouge (de préférence), soit le bleu et on obtient comme précédemment 2 équations à 2 inconnues qu'il suffit de résoudre.

Par exemple avec le véhicule rouge :

Je comprends.

Cela dit j'ai une question, lorsqu'on a établis les projections, Oy vaut 0 car l'objet ne décolle pas du sol ?

Lorsqu'on a dit ça :

Sur l'axe Oy : 0 - P + 0 + R = 0

On écrit que la somme est égale à 0 car l'objet ne décolle pas du sol?  Si on était dans un cas où l'objet évoluerait en hauteur vaudrait-il 0 ?

Oui, on peut le voir de cette manière.

Une analyse plus "physique" consiste à revenir à la deuxième loi de Newton :



qui a pour conséquence que le vecteur accélération a même direction ( et même sens ) que la résultante des forces appliquées au système.

Ou bien ( Ce sera peut être plus clair)

Au lieu d'écrire directement :

D'accord, j'ai compris.

Merci à vous.