tu as déjà du faire des exercices de skieur en physique non ?
pour vérifier tes intuitions, il faut se lancer dans les calculs

Alors tout à fait
En revanche j'ai omis de préciser que cela doit bien faire 15 ans que je n'ai pas eu la chance de suivre un cours de physique et par conséquent pas mal de formule sont assez lointaines ! J'ai posté dans cette section me disant que c'était dans le pgrm

J'ai réussi en farfouillant à identifier une formule :

v(t) = (mg/l).(sin(alpha) - f.cos(alpha)) * (1 - e^((-l/m).t))  [je pourrais fournir le raisonnement qui a permis d'aboutir à ça si besoin], mais je constate juste que plus le poids est important plus la vitesse max est importante. Je ne suis pas sur en revanche que cela prenne en compte la résistance liée à l'air.

Est ce que cette formule est correcte ? Est ce que je dois prendre en compte d'autres paramètres ?  

ah d'accord effectivement je m'attendais plutot à un première S ^^
mon problème avec votre formule est que je ne sais pas ce que représente l ^^
ça serait un coef de frottement visqeux en -l.v ? et f est le coef de la loi de Coulomb pour les frottements neige/ski ?

Discussion.

Composante du poids tangentielle à la piste: |F1| = mg.sin(alpha) (avec alpha l'angle de la piste avec l'horizontale).

Composante du poids normale à la piste: N = mg.cos(alpha)

Avec k1 le coefficient de frottement dynamique (neige - ski), on a la force de frottement neige-ski : |f1| = k1.|N| = k1.mg.cos(alpha)

Il faut aussi tenir compte du frottement aérodynamique (air-skieur) : |f2| = k2.v² (avec v la vitesse su skieur) et k2 une constante dépendant du skieur.

k2 = (1/2).S.Cx.Rho(air) (voir par exemple ici http://fr.wikipedia.org/wiki/Tra%C3%AEn%C3%A9e pour quelques explications).

La résultante des forces sur le skieur tangentiellement à la pente est R = |F1| - |f1| - |f2| et on a aussi R = m.a = m.d²x/dt²

--> m.d²x/dt² = mg.sin(alpha) - k1.mg.cos(alpha) - k2.(dx/dt)²

d²x/dt² = g.sin(alpha) - k1.g.cos(alpha) - (k2/m).(dx/dt)²

C'est l'équation différentielle régissant le mouvement du skieur.

k1 dépend des sksi et de la neige --> avec des skis identiques, sur une même trajectoire, k1 ne dépend pas du skieur.

---> pour l'exercice proposé: d²x/dt² = Constante - (k2/m).(dx/dt)²

Le skieur qui aura la plus grande accélération (et par suite sera le premier en bas de la piste) est celui pour lequel le terme k2/m est le plus petit.

Le "m" de cette expression favorise le skieur "lourd", reste à voir ce qu'il en est de la valeur de "k2" qui dépend du skieur.

k2 = (1/2).S.Cx.Rho(air)

Rho(air) est évidemment le même pour les 2 skieurs.

Reste "S.Cx".
Le S est "normalement" en défaveur du skieur lourd puisque c'est la surface du skieur qui "résiste" à la pénétration dans l'air.
Le Cx ... Ca c'est une autre affaire, il dépend de la "forme" du skieur, sa forme, pas sa taille qui est reprise dans le S.
Un bon skieur qui descend avec la position de l"oeuf" aura un Cx bien plus petit que celui qui descend droit comme un piquet ...

Si on a affaire à 2 skieurs de la même "qualité" et qu'ils ont des positions équivalentes sur leurs skis, alors les Cx sont identiques.
Si on est dans cette configuration, alors seule le rapport S/m intervient (plus il est faible, plus on va vite)

En rappelant que S est la surface du skieur qui "résiste" à l'entrée dans l'air et m la masse du skieur.
Je l'aisse aux spécialistes de l'anatomie décider comment le rapport S/m varie avec la corpulence d'un bonhomme.
-----
Sauf distraction ... et sans relecture.

salut J-P

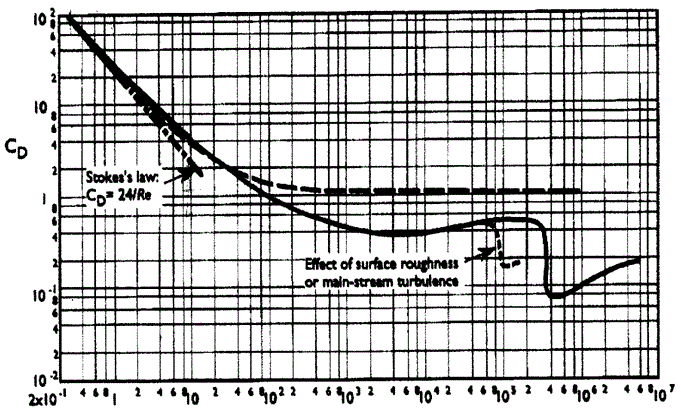
je suis tout à fait d'accord avec ta mise en équation et tes conclusions. J'ajouterais que le Cx est le terme le plus difficile à estimer. Il est fonction du Reynolds selon la courbe que je joins (Re en abscisse et Cx en ordonnée) On peut estimer l'ordre de grandeur du Re pour notre skieur dans les 10^5. C'est pour cela que on peut supposer un Cx relativement constant. Pour des liquides plus visqeux que l'air et des vitesses moindres, on peut avoir des Cx en 1/v ! Le creux soudain dans la courbe est du au passage laminaire/turbulent qui se produira à d'autant plus basse vitesse que l'objet (le skieur ici) est peu aérodynamique. Mais bon en première approximation, gardons un Cx constant ^^

Oui efpe,

MAIS attention.

Les courbes que tu donnes sont pour un "mobile" sphérique... même si ce n'est pas écrit sur ton graphe.

Pour une autre "forme" de mobile, les courbes seront différentes. (elles seront évidemment ressemblantes mais avec un shift en vertical surtout pour les parties quasi horizontales des courbes).

Et donc dans le problème du skieur, la "position" sur les skis du skieur peut avoir un effet très important sur le Cx.

Le Cx qui est de l'ordre de 0,5 (dans le "plat" des courbes) pour une sphère, peut descendre vers 0,3 pour une forme en "oeuf", mais peut aussi remonter vers 1 pour un skieur débutant (droit comme un piquet), avec bien entendu toutes des valeurs intermédiaires depuis les néophites jusqu'aux pros.
  
Ce n'est pas pour rien que les cylistes professionnels spécialistes du contre la montre font des essais en soufflerie ... pour améliorer leur CX par leur position sur le vélo.

Fan-ta-stique !
Aussi inattendu que cela soit, j'ai presque envie de retourner en cours de physique
Déjà un grand merci pour la qualité des réponses et de vos échanges de spécialistes !
Pour répondre à la première question d'efpe, ma formule vient en fait d'un précèdent post sur ce forum reprenant une pbmatique skieur similaire, et pour ne rien cacher, l'auteur (tout du moins sur ce post ^^) de cette formule n'est autre que J.P (le monde est petit quand même ) : https://www.ilephysique.net/sujet-etude-d-un-skieur-232867.html
De là à dire si il s'agit de la loi de Coulomb ou non...

Je vais regarder tout ça calmement ce week end pour faire quelques calculs qui illustreront vos démonstrations, je vais me pencher un peu sur cette question de trainée, et je pense que mon skieur aura une forme d'oeuf ou de boule pour simplifier un peu !
La variation de ma boule/oeuf sera fonction uniquement du poids a densité égale (si je suis logique, la boule la plus lourde sera sensiblement plus grosse et offrira donc une plus grande résistance à l'air ) Je vais également chercher comment faire quelque chose de rationnel ^^

Petites questions tout de même :
Dans R=m.a
A quoi correspond "a"  ? Est ce qu'il s'agit de l'acceleration de mon skieur  ?

Quelle valeur pourrais-je donner à k₁ ?
Est ce que pour un skieur plus lourd ne "s'enfonce" pas plus dans la neige en accroissant donc ce frottement ? Ou bien ce paramètre est-il déjà pris en compte via f₁, cette dernière intégrant la variable "m" ?

d²_x/d_t²... Bon donc si je ne me suis pas trop égaré dans mes recentes recherches d_x/d_t correspond à la dérivée de x par rapport à t ce qui doit me permettre de determiner la vitesse à l'instant t (en m.s^-1 a priori ?)
Je sens qu'il y à de l'intégration dans tout ça, encore que....
Si on dit que  :
m=50Kg
g=9,81m.s^-2
=45°
k₁ = à determiner, mais pourquoi pas 0,5 arbitrairement
on obtient 5,7706 comme valeur de ce que J.P définit comme "constante" dans l'équation
d²_x/d_t²= Constante - ((k₂/m).(d_x/d_t)²)
Jusque là, pas violent.
Mais à quoi correspond concrètement d²_x/d_t² ? à l'acceleration ? en quelle unité cela se trouve ?
et in fine une fois que k₂, donc et ses copains, sera définit, comment obtenir un chiffre ?

Pour tenter une reformulation : je chercherai à déterminer le skieur qui en partant d'un point donné identique sans autre forme d'énergie de départ que la simple gravité, sera le premier dans un premier temps, a quelle moment le second que j'imagine 2nd va rattraper le 1er et quelles seront leurs positions respectives soit au bout de x mètres soit à l'instant t=x

Désolé de toutes ces questions, mais je suis curieux (et plus forcement aussi habile en math/physique que je ne le fut )

En attendant je vais me pencher sur k₂

Je ne sais pas comment éditer le precedent post...
Bref !
Pour le calcul  de k₂ vs le lien wikipedia, je constate qu'il y a la vitesse à prendre en compte aussi apparement :
k₂=1/2C_x..S.V²
avec C_x : le coéfficient dependant de la forme du solide
: la masse volumique du fluide (la notion de fluide me trouble, mais admettons !) --> comment cette masse peut elle être identique entre les 2 skieurs ? (j'ai trouvé une constante 1kg.m^-3, ça coole ? )
S : la section droite perpendiculaire au vent (est ce que je simplifie en prenait l'aire d'un cercle si mon skieur est une boule ? )
V : la vitesse d'écoulement du fluide (vitesse de mon skieur si on considère qu'il n'y pas de vent)

En revanche dans la démonstration de J.P, pas de "V"
J'imagine sans peine que ce n'est pas un oubli, mais du coup, pourquoi pas de "v" dans cet exercice ?

A quoi correspond "a"  ? Est ce qu'il s'agit de l'acceleration de mon skieur  : OUI

Quelle valeur pourrais-je donner à k1 ? : 0 < k1 < 1. Sa valeur dépend de la piste. Si elle est verglacée, k1 est presque nul, pour une piste moins glissante, k1 est un peu plus grand mais en tout cas largement < 1 dans le cas d'un skieur sur une piste enneigée.
Cela suppose quand même qu'il s'agit bien de "glissade", si le skieur est enfoncé dans la neige cela ne va évidemment pas.
Prendre k1 = 0,1 me semble pas trop faux en première approximation.

dx/dt est la vitesse du skieur sur la piste, (dx/dt)² est donc le carré de la vitesse, et d²x/dt² = accélération du skieur (attention de ne pas confondre (dx/dt)² et (d²x/dt²))

Si x est en m et le temps exprimé en secondes, dx/dt (la vitesse) sera en m/s et d²x/dt² (l'accélération) sera en m/s²

Pour k2:
k2 = (1/2).S.Cx.Rho(air)

Rho(air) = 1,3 kg/m³ (environ)
Cx a été un peu discuté avant, on peut prendre Cx = 0,6 en première approximation.
S sera en m², c'est la surface que verrait un bonbomme regardant le skieur lui arriver droit dessus. avec un skieur en position "honnète", S = 0,7 m² me semble par trop faux pour le bonhomme de 80 kg, mais il faut voir comment varie S avec le poids du bonhomme.

Tout cela "au pif" naturellement.

On aura donc le tout en unités SI et pour le skieur de 80 kg:

k2 = (1/2)*0,7*0,6*1,3 = 0,273

d²x/dt² = g.sin(alpha) - k1.g.cos(alpha) - (k2/m).(dx/dt)²

d²x/dt² = g.sin(alpha) - k1.g.cos(alpha) - (k2/m).(dx/dt)²

d²x/dt² = g.sin(alpha) - k1.g.cos(alpha) - (k2/m).(dx/dt)²

d²x/dt² = 9,8.sin(45$°$) - 0,1*9,81*.cos(45$°$) - (0,273/80).(dx/dt)²

d²x/dt² = 6,2 - 0,0034.(dx/dt)²

Et avec v = dx/dt (vitesse du skieur), l'équation devient :

dv/dt = 6,2 - 0,0034.v²

Equation différentielle qu'on peut résoudre ...

On a de suite cependant, sans besoin de la résolution, la vitesse max qui peut être atteinte qui est pour dv/dt = 0 --> (vmax)² = 6,2/0,0034
v max = 43,7 m/s soit 157 km/h

Cela évidemment avec toutes les approximations faites et aux erreurs de calculs près.

A nouveau un grand merci
Un point de détail, je pense avoir correctement refais les calculs, en revanche je ne tombe pas sur d²x/dt² = 6,2 - 0,0034.(dx/dt)², mais sur d²x/dt² = 7.83 - 0,0034.(dx/dt)²...
A cela près, le raisonnement me parait bon (je plaisante^^)
Calculer une variation satisfaisante de S en fonction du poids me semble plus compliqué que ce que j'avais prévu (mais depuis le départ, force est de constater que j'avais mal prévu bcp de choses !)
En gros le skieur le plus lourd ira le plus vite...

pour préciser simplement "l'enfoncement dans la neige", je pensais que la force de frottement neige-ski serait supérieure. Ce qui est le cas, mais finalement dans l'équation les masses s'annulent (dans la première partie en tous cas, la masse reste pour le calcule de k₂/m)

Si je trouve un lien valable entre le poids et la surface, je ferai une commentaire complémentaire ! D'ici là je vais explorer quelques livres de math et repartir dans les dérivées et équations différentielles, je sens que cela a été comme un frein à ma compréhension (et un d'autant plus grand merci d'avoir finalisé le calcul )

9,81.sin(45°) - 0,1*9,81*.cos(45°) = 9,81/V2 - 0,1*9,81/V2 = 0,9*9,81/V2 = 6,2.  

Tu as trouvé 7,83 car tu t'es planté dans l'utilisation de ta calculette. Tu as mis la calculette en mode "radian" au lieu du mode "degrés".

:D
Au fond de moi même je suis rassuré ! Je ne m'expliquais pas que l'erreur puisse venir de vous !

Pour en revenir à mon S.
SI je considère que mon skieur est une sphère d'eau (j'essaye de simplifier encore et toujours pour trouver le raisonnement ^^) :
Le volume de ma sphère sera (4R³)/3
Si je prends la densité de l'eau standard (la bonne temperature, la bonne pression atmosphérique...) soit 1000kg.m^-3 ou 1g.cm^-3 ou encore si je ne me trompe pas 1L d'eau = 1kg.
Donc pour théoriser une boule de 80Kg, il me faut une sphère de 80L ou de 0,08m³.
A priori R = 0,576m permet de trouver ce volume.
Du coup pour calculer S je peux prendre l'aire (d'un cercle de ma sphère) : R² soit 1,042m²
Pour 50kg, R=0,4927m et A=S=0,762m²
Et on conserve C_x=0,6

Est ce que ca pourrait coller ?

k2 est proportionnel à S donc à R² (si on considère une forme sphérique)

m est proportionnelle au volume et donc à R³

---> k2/m est proportionnel à R²/R³ = 1/R

ou si on préfère = (k2/m) est proportionnel à l'inverse de la racine cubique de m

donc si k2/m = 0,273/80 = 0,0034 (SI) pour m = 80 kg, on aura (k2/m) = 0,0034 * (1 / racinecubique(50/80)) = 0,004 (SI) pour m = 50 kg

Avec des volumes proches de sphères (et une masse volumique identique pour les 2 cas).

Avec ces hypothèses, la vitesse max atteinte par le bonhomme de 50 kg serait : v max = racinecarrée(6,2/0,004) = 39,4 m/s soit 142 km/h

Bonsoir,

Tout d'abord merci à vous pour ces démonstrations des plus claires!
Dans la continuité de ce topic, je me posais une question dont je ne trouve pas réponse...
Cela fait maintenant bien trop longtemps que je n'ai plus résolu d'équation différentielle et les mécanismes me manquent...

La démonstration de JP permet de calculer Vlim si je ne m'abuse. Mais pourriez vous m'expliquer comment calculer la vitesse atteinte par le skieur au bout de 300 m par exemple?

J'avoue ne pas savoir comment m'y prendre...

Merci par avance de vos réponses!!!

En repartant de l'équation : dv/dt = 6,2 - 0,0034.v²

dv/(6,2 - 0,0034.v²) = dt

dv/[-0,0034.(v-42,7)(v+42,7)] = dt

dv/[(v-42,7)(v+42,7)] = -0,0034 dt

A.dV/(v-42,7) + B.dV/(v+42,7) = -0,0034 dt

A+B = 0
42,7.(A-B) = 1

A = -B = 0,0117

0,0117.dV/(v-42,7) - 0,0117.dV/(v+42,7) = -0,0034 dt

dV/(v-42,7) - dV/(v+42,7) = -0,29 dt

ln|(v-42,7)/(v+42,7)| = -0,29 t + K

Si v = 0 en t = 0 ---> K = 0

ln|(v-42,7)/(v+42,7)| = -0,29 t

(42,7-v)/(v+42,7) = e^-0,29t

(42,7-v) = (v+42,7).e^(-0,29t)

-v(1 + e^(-0,29t)) = -42,7.(1 - e^(-0,29t))

v(t) = 42,7.(1 - e^(-0,29t))/(1 + e^(-0,29t))
-----

On voit ici que Vlim = 42,7 m/s et 43,7 m/s que je l'avais écrit, sûrement par une faute de frappe dans un précédent message.

Manque encore un bout.

Ci dessus, on a la vitesse en fonction du temps.

Si on veut la distance parcourue en fonction du temps, elle s'obtient en intégrant v(t) ...

Bonjour J-P,

je vous remercie pour votre réponse. Effectivement il me manquait certains outils pour réaliser ce calcul...
Néanmoins je m'interroge sur la méthode pour parvenir à mes fins... en intégrant à nouveau v(t), je vais avoir la distance en fonction du temps...

Je repose donc le problème:
- un skieur m=80 kg
- une distance de glisse AB=309 m
- une pente α=12,79°
- vitesse initiale nulle V(A) = 0

J'aimerais connaitre la vitesse atteinte par le skieur au bout des 309m avec prise en compte des forces de frottements et forces aérodynamiques...

C'est ici un cas concret, une situation vécue et j'aimerais connaitre la vitesse pour en déduire une quantité d'énergie...

Pourriez vous m'éclairer?

Merci par avance!!

On ne peut évidemment pas donner une réponse numérique pile poil à cette dernière question.

Puisque les valeurs de k1 et k2 (voir les messages précédents) ne sont pas connus.

Ils dépendent l'un ou l'autre de l'état de la neige, de la température, du fartade des skis, de la masse volumique de l'air, du fini de surface de la combinaison du skieur, de la position du skieur ...
Bref d'une multitude de paramètres.

Il faut donc prendre des valeurs numériques les moins fausses possibles pour ces paramètres et établir l'équation différentielle donnant v(t) compte tenu de tous ces paramètres.

Une fois cela fait, soit on se tape l'intégration à la mode matheux, soit on le fait à la mode "ingénieur" en calculant via un tableur des variations de v pour de successives variations élementaires de t. Et en profitant des capacités de calculs du tableur pour faire une intégration de v(t), c'est sans réelles difficultés.

Mais évidemment, la précisison de la réponse trouvée pour la vitesse acquise à une distance parcourue données dépendra forcément de la précison de toutes les valeurs des paramètres rappelés ci-dessus (plus ceux non mentionnés).

On peut aussi faire l'étude purement mathématique (intégration suivant les techniques habituelles) en conservant k1 et k2 littérals dans les équations.

Si un matheux veut s'en donner la peine ...
Mais pas moi.