Inscription / Connexion Nouveau Sujet
Skieur en descente
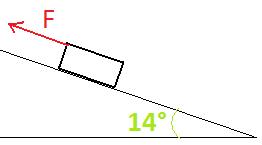
Un skieur de masse m = 90,0 kg(avec tout le matériel) descend une piste inclinée de 14,0° sur l'horizontale à une vitesse constante de 70,0 km.h-1.
Les forces de frottement de la piste sur les skis ainsi que celles de l'air ont une résistante parallèle à la pente.
1. Faire l'inventaire des forces agissant sur le skieur
Eh bien pour moi il y a P (le poids du skieur)
R (la réaction pente/skis)
et F => comme dans l'énoncé
De plus comme le skieur a un mouvement rectiligne uniforme,
donc
2. Le principe d'inertie permet de calculer F de . Pourquoi ? Calculer F.
là je calcule d'abord P, puis je dis que du coup R + F = P
...mais apparemment ce n'est pas du tout ça qu'il faut faire, il faudrait faire des projections sur x ??
merci d'avance pour votre aide 
Bonjour,
1. - Poids P, Ok
- la réaction normale Rn du support et non pas R; car R=Rn+f (en
vecteur) et f figure dans F
- les forces de frottements F avec la piste et ceux dus á l'air
2. Très bonne question:
Disons que: 
+
=
Mais cela ne s'entend pas par: u+v=w
Attention, dans le cas où et sont colinéaires et de même sens, l'egalité u+v=w est correcte.
Dans le cas où et sont colinéaires et de sens opposés, on a:
w= |u-v| (valeur absolue)
Si et ne sont pas colinéaires , aucune des 2 égalités précédentes sont correctes ...
Néanmoins, P est colinéaire avec F+Rn vecteur donc P=- (R+F) mais en vecteur
R et F ne sont pas colinéaire, donc je ne peux pas écrire P=R+F (en module)
Pour calculer F plusieurs méthodes existent...
En notant A la résultante de Rn + F
on obtient: A=P (en module); A=-P (en vecteur) et A=F+Rn (en vecteur) mais A
(F+Rn) (en module)
F et Rn sont deux vecteurs dont leurs directions forment un angle droit; donc d'après pythagore:
A^2=F^2+Rn^2 (en module)
or A=P (en module) donc:
P^2=F^2+Rn^2
(m*g)^2=F^2+Rn^2 [1]
Calculons Rn:
Rn se compensent avec Py donc Rn=Py (en module)
Utilise la trigonométrie pour calculer Py et trouver alors la valeur de Rn
Tu résouds [1] pour trouver la valeur de F (bien évidemment, F doit etre positive)
SI tu es intéressé á connaitre les autres méthodes, je t'envoie á une fiche où les méthodes qu'on peut utiliser sont expliquées de facon explicite; et si tu trouves quelques difficultés á comprendre, n'hesite surtout pas á demander !
Il suffit de cliquer sur la maison:
[lien]
Voici une figure où j'ai mis toutes les composantes et résultantes dont tu as besoin ...
Sauf distraction
Merci beaucoup pour votre aide !!
alors alors...
F^2 = P^2 - Rn^2
=> on a P = mg = 90,0 * 9,81 = 88,3 .10 J
en module, Rn = Ry = Py
or on peut calculer Py :
= Py/P
<=> Py= *P
<=> Py= *88,3 . 10
<=> Py= 85,7 . 10 Joules = Rn
on peut donc résoudre [1] : F = racine (P^2 + Rn^2)
F= racine ( 88,3 . 10^2 + 85,7 . 10 ^2 )
F= 12,3 .10 J
C'est bien ça ?
Re,
P= 883 N Ok
Py=Rn=857 N Ok
Une petite erreur:
Or P^2=F^2+Rn^2
donc F^2=P^2-Rn^2
F=
(P^2-Rn^2)
= 213 N
L'unité Joule (J) est utilisé pour l'énergie et le travail; et l'unité Newton (N), pour l'intensité de la force ...
Annuler
connectez vous