Inscription / Connexion Nouveau Sujet
skieur
bonjour, pouvez vous m'aider s'il vous plait!
un skieur chaussé de ses skis ( de masse m =90kg) remonte une piste en téléski. Le système mécanique étudié est l'ensemble(skieur+skis). Il y a des frottements sur la neige. La force de frottement F a la meme direction que le vecteur vitesse et le sens inverse, l'intensité de F est égale à 30N.
La remonté en teléski correspond à un déplacement AB de longueur 1250m; le plan de la remontée forme un angle a= 20° avec l'horizontale.
1) compléter le schéma fourni en annexe en représentant les forces s'exerçant sur le système.
j'ai mis le poids, la force exercée par la tige, la réaction normale du sol, les forces de frottements.
2)calculer le travail Wp du poids P du système lors du déplacement considéré. On prendra g=10N.kg
j'ai mis que W(P)= -(m*g)*AB*sin a
et j'ai trouver -377 462 J en prenant g=9.81 est-ce bon?^^
3)calculer le travail Wf de la force de frottement F lors du déplacement considéré. et j'ai trouvée - 37 500 J c'est bon ?
4) Dans ces conditions, quel est le travail Wr de la réaction R du support du système ? j'ai trouvé 0 car perpendiculaire au sol.
5)Calculer le travail Wt de la tention T du cable qui tire le skieur sachant que son intensité est de 675N et que la direction du cable fait avec le plan incliné un angle 
= 60° je ne sais pas !
voila merci d'avance et m'aidez si je me suis trompé... je ne sais pas si j'ai juste avec les angles sachant que 
= 20° et = 60°
Bonjour,
2)
"j'ai trouvé -377 462 J en prenant g=9.81 est-ce bon?"... Dans l'énoncé, on dit de prendre g = 10 N.kg-1 !!
Wp = -384772 J
3) WF = -37500 J
4) C'est bon ==> R perpendiculaire au déplacement
5)
On peut décomposer la tension du câble en 2 forces, l'une parallèle au plan incliné (la piste)(c'est celle qui travaille) et l'autre perpendiculaire au plan incliné (qui ne travaille pas car perpendiculaire au déplacement).
WT = (675 x cos(60)) x 1250 = 421875 J
Mais il y a quelque chose qui m'ennuie...
Sur la perpendiculaire à la piste, on a R + T sin - P cos = 0 ==> pas de problème
Sur la parallèle à la piste, on a -P sin - F et T cos
Or : -P sin - F 
337,82 N avec g = 10
Et : T cos = 675 x cos(60°) = 337,5 N
Donc le skieur ne peut pas remonter la pente !!...
Me serai-je trompé quelque part ?...
Evidemment, si on prend g = 9,81, ça arrange bien les choses :
-P sin - F 331,97 N
Donc, avec g = 9,81 N.kg-1 :
Wp -377,462 J
WF = -37500 J (ça ne change pas)
WR = 0 (ne change pas)
WT = (675 x cos(60)) x 1250 = 421875 J (ne change pas)
Donc, là, le skieur peut remonter parce que T cos > P sin + F (337,5 N > 331,97 N)
Pourquoi disent-t-ils de prendre g = 10 N.kg-1 ? Mystère...
sauf erreur de ma part...
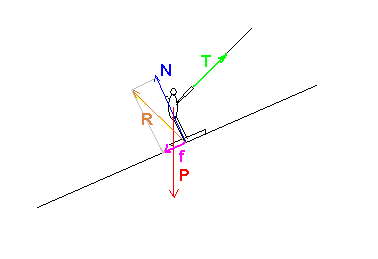
(dessin pas à l'échelle).
2)
Wp = mg.Deltah = 90 * 10 * (-1250*sin(20°)) = -384773 J
3)
Wf = - 30 * 1250 = -37500 J
4)
La réaction du support à une composante normale au sol (N) mais aussi une réaction due aux frottements (et oui, c'est bien le sol qui provoque ces frottements en frottant sur les skis).
--> Wr = - 37500 J
5)
Wt = 675 * cos(60°) * 1250 = 421875 J
On aurait du trouver que Wt + Wp + Wf = 0, soit Wt = 384773 + 37500 = 422273 J
Ceci est du à l'imprécision des données du problème (erreur de l'ordre de 0,1 %)
-----
Sauf distraction. 
Annuler
connectez vous