Bonsoir,

Je suggère qu'après avoir fait un schéma, tu appliques le théorème de l'énergie cinétique deux fois .

Une première fois entre les points B et C pour obtenir la vitesse en B
Une deuxième fois entre les points A et B pour répondre à la question posée.

Qu'en penses tu ?

Sûrement une excellente, je vais essayer, mais je ne suis pas sur d'y arriver, je pense que je remettrai un post d'ici peu car je n'ai pas réussi 😅 mais avant, j'essaye tout de même !

Excellente idée *

Conseil :
Pour chacune des deux phases du mouvement du skieur il est indispensable de faire l'inventaire des forces qui s'exercent sur lui, car ces forces ne sont pas toutes les mêmes d'un phase à l'autre.

Oui effectivement j'ai trouvé en force de A vers B :force de frottements (résistantes), réaction du support (nulle), poids (nulle) et traction (moteur)
Pour b vers c j'ai mis reaction du support (nulle) poids (résistant) et la vitesse initiale (moteur)
Ensuite :après plusieurs tentatives, je trouve Vb=p(2Ec/m)^1/2
Mais je n'arrive pas à aller plus loin

Vb=(2Ec/m) ^1/2, il n'y a pas le p de la réponse ci dessus

As tu fait un schéma ? Tu peux le scanner ou le photographier et le poster.
Il me permettra de comprendre les erreurs que tu commets car il y a en effet des erreurs dans ton analyse des forces :

De A vers B : Il y a bien les 4 forces que tu décris mais aucune de ces forces n'est nulle !
Il me semble que tu confonds intensité d'une force avec travail de cette force.

De B vers C :
La réaction du support n'est pas nulle
La dernière force dont tu parles (vitesse initiale), n'existe pas : La vitesse n'est pas une force.
Il n'y a que deux forces qui s'exercent sur le trajet BC

Cela fait tu pourras appliquer le théorème de l'énergie cinétique deux fois :
Une fois entre A et B, une autre fois entre B et C
Dans mon précédent post le suggérais de commencer par la partie BC, ce n'est pas une obligation, tu peux commencer par la partie AB

L'important est d'obtenir deux équations : Une pour chacune des parties du trajet.
On verra alors comment combiner ces deux équations pour répondre finalement à la question posée.

Mais j'ai vu en cours que la réaction du support est toujours perpendiculaire au mouvement et que son travail est nul ?

Voici mon schémas. Mais j'ai trouvé des intensités nulles pourtant, cela ne signifie pas que le travail est nul ?

.

** image supprimée **

Une force d'intensité nulle (zéro Newton) est une force qui n'existe pas.
La réaction du support est une force qui existe, elle a une intensité qui n'est pas nulle.
En revanche comme elle se déplace perpendiculairement à sa propre direction cette force ne travaille pas. Son travail est nul.

Sur mon schéma ci-dessous les échelles ne sont pas respectées pour gagner en clarté.
Le skieur nautique a été réduit à son centre de gravité G

Mais dans le calcul on ne prend pas en compte la réaction du support si  ?

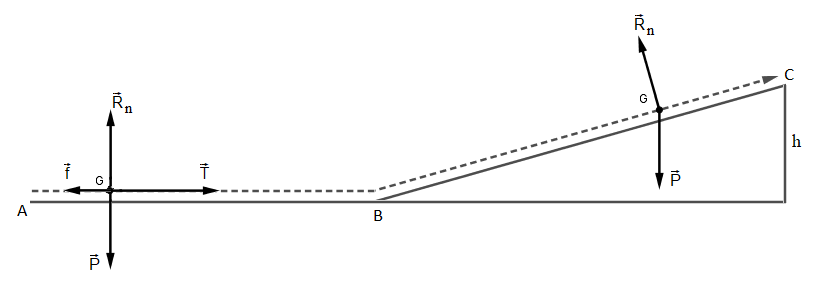
En effet, que ce soit sur la partie AB du trajet comme sur la partie BC, la direction de la réaction du support est perpendiculaire à celle du déplacement.
Il en résulte que cette force a bien un travail nul, mais ce n'est pas une raison pour écrire comme tu l'as fait dans ton post du 11-05-20 à 00:20 que cette force est nulle !!!

En résumé :
Si une force est nulle (donc n'existe pas) , son travail est évidemment nul
mais
Si une force a un travail nul, elle n'est pas nulle pour autant ! Ecrire qu'elle est nulle est alors une grosse faute.

Ah d'accord pardon ^^' donc comment que dois-je dire dans mon bilan des forces au sujet de la réaction du support ?

La force est perpendiculaire au déplacement
Cela justifie que son travail est nul.