Inscription / Connexion Nouveau Sujet
satellite géostationnaire
Bonjour j'ai une exercice à faire pour demain pouvez vous m'aidez svp ?
un satellite géostationnaire est situé dans le plan de l'équateur à 35 700 km d'altitude. Il paraît immobile dans le ciel pour un observateur situé à la surface de la Terre. Dabs le référentiel géocentrique on précise qu'un point de la surface de la terre fait un tour complet en 86 164 s. L e rayon terrestre vaut 6400 km.
1)Quel est le mouvement su satellite (noté S) dans el référenciel géocentrique ? dans le référentiel terrestre ?
2)Faire un schéma du système Terre-satellite vu depuis une étoile fixe situé dans l'espace, très loin au dessus du pôle Nord( on doit voir la terre , le satellite et l'orbite du satellite)On représentera le rayon terrestre par une longueur de 1 cm.
3a)calculer la longueur de la trajectoire du satellite.
b) en déduire sa vitesse dans le référentiel géocentrique.
4a) Dans un référentiel terrestre représenter le trajet suivi sur un signal radio partant d'un point A sur l'équateur, ??(je ne vois pas ce qui est écrit sur ma feuille) par le satellite S situé à la verticale de A qui le ???????????????????????????????????????????????????(ce qui est écrit est effacé sur ma feuille) renvoi vers un point B également sur l'équateur et situé à 3000,00km de A.
b) Quelle est la durée nécessaire pour que le signal effectue le trajet de A et B ? on considérera que le triangle SAB est rectangle en A.
c)Comparer cette durée avec celle que mettrait le signal pour aller directement de A et B en ligne droite, sans passer par S.
Donnée:
Vitesse d'un signal radio dans l'air: c=3.00 X 108m.s-1
Bonjour,
1) Dans le référentiel géocentrique, le mvt du satellite est circulaire uniforme
Dans un référentiel terrestre le satellite apparaît immobile pour un observateur
(c'est la définition d'un satellite géostationnaire)
2) Je ne peux pas le faire à ta place.
3) La distance du satellite au centre de la Terre est r = Rayon de la Terre + altitude z du satellite
Donc r = 6400 + 35700 km
La trajectoire étant circulaire, le périmètre du cercle parcouru est 2
r
La durée pour parcourir ce cercle est de t=86 164s.
Donc tu peux en déduire la vitesse v (attention aux unités!!)
4) Si c'est "effacé" je vais avoir du mal à traduire l'énoncé 
D'accord merci beaucoup pour votre aide 
voici la question 4 je crois que c'est sa 
ans un référentiel terrestre représenter le trajet suivi sur un signal radio partant d'un point A sur l'équateur,par le satellite S situé à la verticale de A qui le renvoi vers un point B également sur l'équateur et situé à 3000,00km de A.
4)
a)
En devinant ce qui est effacé de l'énoncé:
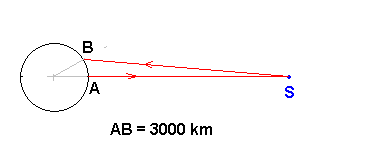
Avec les approximations permises par l'énoncé:
AB² + AS² = BS²
3000² + 35700² = BS²
BS = 35826 km
Trajet total via le satellite = 35700 + 35826 = 71526 km
b)
Durée mise par le signal pour passer de A à B via le satellite = 71526 /3.10^5 = 0,238 s
c)
durée pour que le signal passe directement de A à B = 3000/(3.10^5) = 0,01 s
Soit environ 24 fois plus court que via le satellite.
Sauf distraction. 
Annuler
connectez vous