Niveau première

Resistance en paralléle

Posté par
lechacal2 20-10-10 à 19:30

pouvez vous m'aidez svp, j'y arrive vraiment pas merci

deux résistors de résistances respectives R ohms et (R - 3) sont montés en parallèle. calculer une valeur approchée a 10^-2 prés de R POUR QUE LA RESISTANCE EQUIVALENTE SOIT DE 3 OHMS

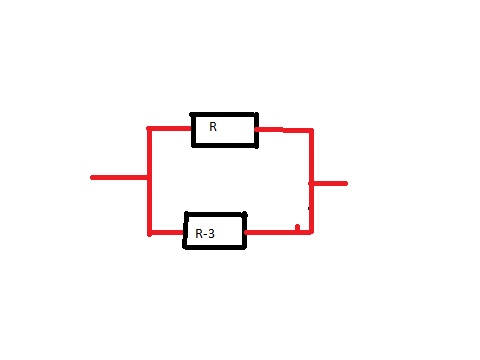
Resistance en paralléle

Posté par re 20-10-10 à 19:34

je suis bloqué a la resolution de

1/Req = 1/R1 + 1/R2 --> 1/3 = 1/R + 1/R-3

Posté par re : Resistance en paralléle 20-10-10 à 19:42

Bonsoir,
$\frac{1}{R_{eq}}\,=\,\frac{1}{R}\,+\,\frac{1}{R-3}\,=\,\frac{1}{3}$
ou :
$R_{eq}\,=\,\frac{R(R-3)}{2R-3}\,=\,3$
$R^2-3R\,=\,6R-9$
$R^2-9R+9\,=\,0$
Donc calcul du discriminant :
$\Delta\,=\,9^2-(4\times 1\times 9)\,=\,81-36\,=\,45$
$sqrt{\Delta}\,=\,3sqrt{5}$
Donc les racines sont...
Tu peux peut-être finir...

Posté par re 20-10-10 à 20:18

merci, lorsque je fais les formules

-b + / 2a je trouve environ -1.15

-b - / 2a je trouve environ -7.85

C'est impossible car la valeur d'une résistance ne peut être négative ...

Posté par re : Resistance en paralléle 20-10-10 à 20:35

Non, les deux racines sont positives. Cela se voit avec les coefficients du trinôme.
$R_1\,=\,\frac{9+3sqrt{5}}{2}\,=\,\frac{3}{2}\,(3+sqrt{5})$
$R_2\,=\,\frac{9-3sqrt{5}}{2}\,=\,\frac{3}{2}\,(3-sqrt{5})$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau première
46 fiches de physique - chimie en première disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Resistance en paralléle

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique