Inscription / Connexion Nouveau Sujet
Relations entre poids et masse
Bonjour j'ai besoin d'aide pour cet exercice le plus rapidement possible
S'il vous plaît
Un ressort accuse une longueur de 11cm et 15cm respectivement sous l'action de 0,5kg et 2kg.
1- En déduire la constante de raideur du ressort et sa longueur à vide.
2- Pour quelle masse le ressort accuse-t-il une longueur de 17cm ?
3- Evaluer la longueur du ressort sous l'action d'une masse de 3kg.
Données : Prendre g = 10N/kg
Bonjour,
Tu es sur le forum depuis un petit moment déjà, tu sais bien qu'on ne fera pas l'exercice à ta place :
As-tu regardé des fiches de cours qui pourraient te rappeler les notions utiles pour l'exercice ?
Des sujets similaires déjà traités sur le forum ?
Bref, on attend tes pistes de réflexion pour poursuivre l'échange.
Bon après-midi
Je m'excuse , j'étais un peu préssé car j'avais d'autres exercices à traiter
Je sais que la constante de radiateur
K=mg/L-Lo
Mais on me demande de calculer Lo (la longueur à vide)
Je sais que la constante de radiateur
Attention à ne pas prendre trop chaud alors !
Il s'agit de la raideur

Ensuite il faut que tu expliques comment tu as obtenu cette relation :
en définissant les notations utilisées ...
Ensuite, tu es en mesure d'isoler
Il faudrait que tu fasses attention à la qualité rédactionnelle :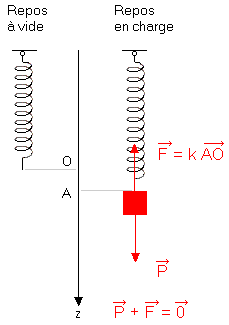
- Système : {ressort + masse}
- Référentiel : le sol, référentiel terrestre
- Bilan des forces :
* le poids du système, de valeur P = m.g ;
- la force de rappel du ressort, de valeur F = k.(L-Lo) si k est la raideur du ressort, Lo sa longueur à vide et L sa longueur lorsqu'il est soumis au poids de la masse.
- Le système est à l'équilibre, donc d'après le principe d'inertie
Tu as deux conditions fournies par l'énoncé :
Cas 1 : le ressort accuse une longueur de sous l'action de
L'équation devient
Cas 2 : le ressort accuse une longueur de sous l'action de
L'équation devient
Tu as donc le système de deux équations à deux inconnues à résoudre :
J'ai essayé
1) calculons la constante du radiateur k
K=P1-P2/L1-L2
P1=m1×g
P1=5N
L1=11 et L2=15
K=5-20/11-15
K=3.75N
Calculons la longueur à vide Lo
mg=P=k(L-Lo)
P1=k(L1-Lo)
P1=5N et k=3.75
5=3.75(11-Lo)
5=41.25-3.75Lo
Lo=41.25-5/3.75
Lo=9.6cm
Je soustrais les deux équations :
En remplaçant ensuite dans l'une des deux équations :
Pour les applications numériques, l'unité SI d'une raideur de ressort est

Je soustrais les deux équations :
En remplaçant ensuite
Pour les applications numériques, l'unité SI d'une raideur de ressort est

Merci j'ai trouvé la même chose Lo=9.6cm
Vraiment merci de tout cœur
Je pourrais maintenant continuer le reste sans problème
Je soustrais les deux équations :
En remplaçant ensuite
Pour les applications numériques, l'unité SI d'une raideur de ressort est

Mais est ce que tu pourrais m'aider pour une petite question


 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site
