Les *** effacé *** chui en terminal en algérie et on nous à jamais parler de sa en 2nde désolé peu pas t'aidé

Edit Coll : la vulgarité n'est pas admise dans ce forum

Tkt !

Un p'tit blocage, notre prof ns a demander de réfléchir à cette question mais moi j'avais envi d'essayer alors voilà :
Un rayon de lumière frappe une surface en Plexiglas (n=1,49) sous un angle d'incidence a .
Trouver sa valeur pour que les rayons réfléchis et réfractes soent perpendiculaire ?
J'ai des p´tites idées mais pas sur du tout....
Merci d'avance !

*** message déplacé ***

Bonjour quand même...

Rappel : le multi-post n'est pas toléré dans ce forum.
 

Personne?? ....

Tu pourrais peut-être poster tes "petites idées"...

Quant à la politesse, elle n'est pas interdite et même plutôt conseillée.
 

Bonjour Coll, merci de répondre !
J'ai le début, je pense...
Alors, n1*sin a = 1,49*sin i2
Donc sin i2 = sin a/1,49
Après c'est la, ou ça ce corse un peu !
Dans l'attente, de ta réponse !
Merci d'avance !

Eh bien maintenant il faut introduire la perpendicularité.

Quelle est la relation entre a et i₂ si l'on veut que les rayons réfléchi et réfracté soient perpendiculaires ?
D'abord commencer par faire un dessin...

Justement j'en ai fait un ! Ça m'a donné des relations :
a= sin a/1,49 + D ! D étant l'angle entre a et le rayon réfracté !
Sin a / 1,49 + D + R ( angle réfléchi) =90 degrés , je dois très certainement passé à côté d'un relation plus importante mais je ne vois pas laquelle...

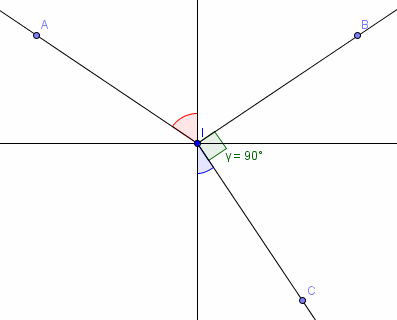
AI est le rayon incident
l'angle rouge est l'angle d'incidence

IB est le rayon réfléchi

IC est le rayon réfracté
l'angle bleu est le l'angle de réfraction

l'angle CIB a pour mesure 90°

Ah d'accord, je comprends mieux , merci !
Mais après voilà, je suis toujours bloqué ... Je sens qu'il faut j'utilise l'angle y ...

Il faut évidemment établir (par la géométrie) une relation entre l'angle d'incidence et l'angle de réfraction.

Puis reporter cette relation dans la loi de Snell-Descartes.

Et enfin, la connaissance des formules élémentaires de trigonométrie fera le reste...

Ça parait tellement simple, dit comme ça !

Soit r l'angle refracté
Cos ^{[/sup]r= 1-sin [sup]} r
Ça peut être utile ça non?
..

"Sup "= au carré

Quelle est la relation (propriété très connue de géométrie) entre l'angle d'incidence (rouge), l'angle de réfraction (bleu) et un angle droit ?

Indice : que vaut l'angle de réflexion (je l'ai laissé en blanc) ?

180 degrés- (90 + angle d'incidence) ? (Je suis pas du tout bon en géo ...)
encore merci du temps que tu prends !

Dans ces conditions ce sera difficile de faire facilement de l'optique géométrique...
___________

Ce que tu as écrit n'est pas une relation.

Je cherche une égalité dans laquelle on trouve les mesures des angles d'incidence et de réfraction ainsi que 90° (si les mesures sont en degrés) ou /2 si les mesures sont en radians.

Nouvel indice : ma figure est "exacte" : les angles ont les mesures attendues...

On voit ça au collège, cette relation ! Parce que sinon j'ai rien vu de tel ! Mais ça ne m'empêche de réfléchir....

*?

Bien sûr (et autrefois on voyait cela à l'école primaire...)

Ok, je suis pire que lamentable ! Je cherche ...

Que vaut l'angle de réflexion (angle blanc entre la normale en I et le rayon réfléchi IB) ?

Je suis sûre c'est super simple en plus !

Oui, et c'est dans le cours d'optique.
Loi de la réflexion...

Mais après angle de réflexion=angle d'incidence mais pour l'instant on en a pas besoin?

On peut souvent faire autrement. Mais quand on dispose d'une solution simple, pourquoi chercher à faire compliqué ?

L'angle de réflexion est égal à l'angle d'incidence

Donc, l'angle blanc est égal à a

La propriété de géométrie :
que vaut la somme

angle de réflexion (angle blanc) + angle (angle vert) + angle de réfraction (angle bleu) = ... ?

Je suis tout a fait d'accord !
180 degrés !

Donc, que vaut la somme
angle d'incidence (a) + angle de réfraction (i₂) = ... ?

Ah oui , 90 degré !

Donc a= 90-i2 non?

Oui !

a + i₂ = 90°

Que vaut i₂ en fonction de a ?

Tu utilises ce résultat dans la relation

1 sin(a) = 1,49 sin(i₂)

et cela va devenir intéressant...

I2=90 - a

Donc, 1 x sin(a) = 1,49 x (90-a)  ??

Donc sin(a) = 1,49 x (90-a)

* sin(90-a)

i₂ = 90° - a

donc :

sin(a) = 1,49 sin(90° - a)

Une petite formule de trigonométrie maintenant pour remplacer sin(90° - a) par quelque chose de plus simple...

D'accord pour ta correction de 18 h 30

Celle qui dit ^cosi2 + ^sini2 = 1

*sin²i2 + cos²i2

sin(90° - a) = ... ?
ou

C'est bien ce qu'il me semblait !
Euh je vois pas !  (Sin 90 - sin(a)) ?

Va voir cette fiche : (Lien cassé)

Donc sin(90-a) = sin 90 x cos a - cos 90 x sin a !?

Ça représente quoi la lettre grec, têtha ?

représente un angle quelconque.
__________

Tu n'as pas choisi la formule la plus simple, mais on fera avec...

sin(90°) = 1
cos(90°) = 0

donc... sin(90° - a) = ...

Sin(90-a) = cos a !

Oui !

Et cette formule de trigonométrie se trouve en bonne place dans la fiche dont je t'ai donné le lien.

sin(90° - a) = cos(a)
__________

Revenons à notre exercice :

sin(a) = 1,49 sin(90° - a)

sin(a) = 1,49 cos(a)

Comment continuer ?

Je vois pas du tout ! Il faut la résoudre là?