Inscription / Connexion Nouveau Sujet
réflexion totale
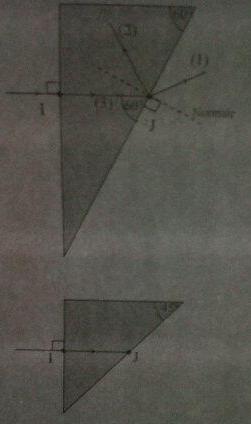
Un rayon lumineux pénètre dans un prisme en verre, par l'une des faces. voir schéma ci-contre.
1.pourquoi ce rayon n'est il pas dévié en entrant dans le prisme?
2. en arrivant sur l'autre face, ce rayon subit une réfléxion partielle et une réfraction.
a ) qu'appelle-ton réfraction?
b )repérer le rayon incident, le rayon réfléchi et le rayon réfracté
c )repérer sur le schéma l'angle de réfraction r, l'angle de réflexion i' et l'angle d'incidence i. donner la valeur de ce dernier.
3. on remplace le prisme précédent par un prisme dont la section est un triangle . Voir schéma
a ) sachant que l'angle limite de la reflexion totale est égale à 42°, la lumiere est-elle totalement réfléchie au point J? justifier
b )terminer le tracé de la marche du rayon lumineux jusqu'à sa sortie du prisme.
Edit Coll : image recadrée
BONJOUR,
As tu cherché à répondre aux questions? Donnes voir les réponses que tu as trouvé pour qu'on puisse voir ensemble qu'est ce qui te bloque.
1) jene sait pas
2) a) Ce qu'on appelle réfraction est le changement de direction que subit la lumière lors du passage d'un milieu transparent vers un autre milieu transparant.
b) le rayon inscident est la droite 1
le rayon reflechit est la droite 2
le rayon réfracté est la droite 3
c) je ne sait pas
3.a) je ne sait pas non plus
b) je l'ai deja fait
Alors pour la question 1 tu as du voir les lois de Snell-Descartes en cours qui sont :
1°Le rayon réfléchit appartient au plan d'incidence.
2°Il y a une relation entre l'angle réfléchit et l'angle incident: i=r on parle des angles entre la normale au dioptre (droite fictive perpendiculaire au dioptre=surface séparant deux milieux) et des rayons en questions.
3°S'il existe, le rayon réfracté appartient au plan d'incidence.
4°Il y a une relation entre l'angle réfracté et l'angle incident: n1.sin(i1)=n2.sin(i2)
Bon dans la première question on s'occupe de la réfraction donc la 4° loi, on voit que le rayon incident arrive sur le dioptre avec un angle i1=0° car le rayon est confondu avec la normale au dioptre.
Donc on a sin(i1)=sin(0)=0
donc n2.sin(i2)=0
Comme n2 est différent de 0, alors sin(i2)=0 ce qui veut dire que i2=0°, le rayon n'est pas dévié.
2)a)Ok
2)b) Je n'arrive pas bien à lire les numéros sur la figure mais si je ne me trompe pas c'est (3) à gauche (2) en haut et (1) à droite c'est ça ?
Le rayon incident est celui qui arrive sur la surface, il suffit de regarder le sens des flèches sur les rayons lumineux. On voit ici que la lumière vient de la gauche du prisme et se propage vers la droite.
Le rayon incident est la droite (3), le rayon réfracté est la droite (1).
2)c) Alors pour ce qui est des angles, il faut repérer la droite en pointillé c'est elle que l'on appelle normale au dioptre. Pour le rayon incident, l'angle d'incidence est l'angle que fait le rayon incident avec la normale au dioptre. En gros sur le dessin c'est l'angle qui se trouve au dessus du (3). J'espère que c'est assez clair. Essaies de trouver les autres angles.
3)a) On veut savoir si l'angle entre la normale au dioptre, au point J, et le rayon incident est plus grand que 42° ou non pour savoir s'il y a réflexion totale.
On va déjà commencer par travailler dans le plus grand des triangles, on connait 2 angles sur les 3, il faut trouver le dernier (situé en bas de la figure). Ensuite on cherchera l'angle restant dans le petit triangle (au point J donc). Si on connait cet angle, on peut trouver la valeur de l'angle fait par le rayon incident et la normale au dioptre en sachant qu'un angle plat est de 180°. Enfin bon on verra ça quand tu y seras...
3)b) Cela dépendra de la réponse à la question d'avant.
Tu as compris mes explications? Est ce que tu as réussi à répondre aux autres questions? Tu peux toujours poster tes résultats et je te dirais si c'est juste ou non.
Est ce que tu as compris le fait que l'on définisse les angles incidents, réfléchit et réfracté par rapport à la normale au dioptre?
Si c'est le cas, un rayon arrivant perpendiculairement à une surface forme donc avec la normale au dioptre un angle de 0°. Jusque là ça va ?
On connait la relation : n1.sin(i1)=n2.sin(i2) n1: indice de réfraction du milieu 1; i1: angle incident; n2: indice de réfraction du milieu 2; i2: angle réfracté.
Si i1=0°, sin(i1)=sin(0°)=0 c'est de la trigonométrie tout simplement.
Si sin(i1)=0 la relation : n1.sin(i1)=n2.sin(i2) devient n1*0=n2.sin(i2) Ca va toujours ?
Donc on peut écrire: n2.sin(i2)=0 comme on sait que n2>1, on a : sin(i2)=0 Or le sinus d'un angle est négatif si l'angle est égal à 0.
Donc si i2=0° l'angle est également confondu avec la normale au dioptre donc le rayon traverse la surface en allant tout droit.


