Inscription / Connexion Nouveau Sujet
Rayon lumineux incident
Bonjour, vous pourriez s'il vous plait m'aider a une question j'arrive pas a la mettre en application. Pour info c'est la question 4 je n'arrive pas. MERCI d'avance
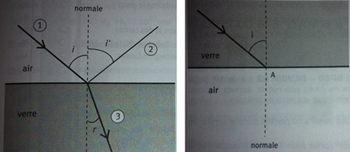
1. Identifier sur le schéma suivant (voir image n°1) le rayon incident, le rayon réfracté, le rayon réfléchi.
- n°1: rayon incident / n°2: rayon réfléchi / n°3 : rayon réfracté.
2. Le rayon réfracté est-il dans le plan formé par le rayon indicent et la normale?
- Oui(voir loi de Snell Descartes )
3. Exprimer sinr en fonction de n0,n sini calculer l'angle r. Donnée : i = 55°.
- Milieu 1 est l'air donc n1= 1,0 et i1= 55° et milieu 2 est le verre donc n2= 1,50 et i2 est l'angle de refléction qu'il faut calculer.
4.Le rayon lumineux incident est maintenant situé dans le verre avec i = 55°.
Observera-t-on le phénomène de réflexion totale? Justifiez la réponse de manière précise.
Tracer le " trajet " du rayon lumineux après le point A. (voir image n°2)
5. Citer une application de la réfection totale en médecine.
En médecine la fibroscopie est une application de la réflexion totale qui est un examen médical permettant de visualiser l'intérieur du corps.
Bonjour,
Bienvenue sur l'  pour ton premier message !
pour ton premier message !
Tout ce que tu as fait est bon.
Quelle est ta réponse à la troisième question ?

Il faut appliquer la loi de Snell-Descartes
n1.sin(i1) = n2.sin(i2)
Tu connais n1, i1 et n2 : cela te permet de calculer i2

Désolé comme je t'ai dit sa fait une semaine que je suis sur cette exercice sans plus j'ai plus reussi a avancé plus
Que vaut n1 ? n1= 1,0
Que vaut i1 ? i1= 55°
Que vaut sin(i1) ?
Que vaut n1.sin(i1) ?
Que vaut n2 ? n2= 1,50
Je ne comprends pas.
De toute façon, sur ton ordinateur tu as une calculatrice.
Impossible de faire ce type d'exercice sans calculatrice !

Non je pense que tu as pas compris moi j'ai fait la question 1 et 2 et 5 et une amie ma aidé pour les calculs
Donc, si ton amie a fait les questions 3 et 4 pour lesquelles il y a des calculs, c'est que tu as fini...


Ta calculatrice calcule avec des mesures d'angles en radians. Il faut la paramétrer pour calculer avec des mesures d'angles en degrés
Tu peux vérifier qu'elle est bien programmée en faisant sin(30°). Tu sais que tu dois trouver 0,5

Il ne faut pas arrondir les résultats intermédiaires.
Que vaut sin(i2) ?
Il faut bien sûr que tu utilises la loi de Snell-Descartes.

Non justement je connais:
- n1.sin(i1)= 1,0 sin(55°)
- n2.sin(i2)= 1,50 sin(?)
désolé si je t'embête mais sa m'aide a comprendre 
n1.sin(i1) = n2.sin(i2)
1,0  sin(i1) = 1,50
sin(i1) = 1,50  sin(i2)
sin(i2)
1,0  sin(55°) = 1,50
sin(55°) = 1,50  sin(i2)
sin(i2)
1,0  0,819 152 = 1,50
0,819 152 = 1,50  sin(i2)
sin(i2)
0,819 152 = 1,50  sin(i2)
sin(i2)
Que vaut sin(i2) ?

Je crois que je vais laissez tomber cette question sur mon devoir car je suis incapable de le faire cette question merci pour tout quand même je suis désolé d'avoir pris ton temps je pensais pouvoir réussir cette question mais IMPOSSIBLE je ferai seulement les question 1, 2 et 5 
Normalement je pense avoir trouvé
1,50 sin(i2) = 0,819 152
n1.sin(i1) = n2.sin(i2)
1,0 sin(i1) = 1,50 sin(i2)
1,0 sin(55°) = 1,50 sin(i2)
1,0 0,819 152 = 1,50 sin(i2)
0,819 152 = 1,50 sin(33,1°)
Que vaut sin(i2) ? c'est sin(33,1°)
Ah merci beaucoup pour tout tes explications sa ma beaucoup aidé pourrez tu faire de même pour la question 4 s'il te plait ? 

Le début de la réponse à la question 4 est absolument similaire à celui de la question 3.
Donc, tu devrais savoir la faire maintenant, au moins savoir la commencer...

4.-Observera-t-on le phénomène de réflexion totale? Justifiez la réponse de manière précise.
Donc étant donnée du resultat oui on aura réflextion totale car n1.sin(i1) = n2.sin(i2)
\large \sin(i_2)\,=\,\frac{n_1\,\times\,\sin(i_1)}{n_2}
Donc étant donnée du résultat oui on aura réflexion totale car:
- n1.sin(i1) = n2.sin(i2)
- sin(i2) = n1  sin(i1) / n2
sin(i1) / n2
Tu ne peux pas répondre avant d'avoir fait l'application numérique.
Quelles sont les valeurs, dans cette question 4, de
n1 = ?
i1 = ?
n2 = ?

Je t'ai posé des questions pour cette question 4, donc avec la figure 2 !
Quelles sont les valeurs, dans cette question 4, de
n1 = ?
i1 = ?
n2 = ?

Pas tout à fait.
Je suis d'accord avec :
n1 = 1,50
n2 = 1,0
Mais je ne suis pas d'accord avec la valeur de i1
Il faut lire, relire... l'énoncé et faire attention à ce que l'on fait !
Le rayon lumineux incident est maintenant situé dans le verre avec i = 55°





