Bonsoir
Il faut bien faire la différence entre système fermé  (vase clos ) dont tu connais sûrement l'étude et la thermodynamique des systèmes ouverts où le fluide circule en régime permanent. On raisonne alors en quantités massiques.  Le premier principe devient alors  :
h=q+w'  où D'accord est le travail technique massique  c'est à dire le travail reçu de des parties mobiles de la machine (compresseur...). On montre que le travail technique massique élémentaire dans le cas de la réversibilité s'écrit :
w'=v. dP  et surtout pas  -P. dV.
Bref: il te faut commencer par revoir un cours structuré sur la thermodynamique des systèmes ouverts en régime permanent.

Écrit avec un simple portable avec correcteur automatique...w' est le travail technique massique...

Bonjour,
Merci pour votre réponse. Je reprendrais mon cours sur les systèmes ouverts en régime permanent, merci pour le conseil.
Par contre pour l'exergie je doute que ça a une relation avec les systèmes ouverts. Pouvez-vous m'expliquer s'il vous plait ? J'ai cherché sur google mais cela ne m'a pas grandement aidé.
Merci d'avance.

Je complète mon précédent message qui, effectivement, était loin de répondre à toutes les questions que tu as posées.

J'avais commencée par les systèmes ouverts. Je précise un peu.

Imagine un système ouvert avec une entrée (indice 1) et une sortie (indice 2) et applique le premier principe de la thermo au système fermé constitué d'un kilogramme de fluide entre son entrée et sa sortie d'une machine. Je suppose le régime permanent et je néglige la variation d'énergie cinétique macroscopique et la variation d'énergie potentielle massique due à une éventuelle variation d'altitude. J'utilise des lettres minuscules pour les grandeurs massiques :



q : quantité de chaleur reçue par 1kg de fluide en traversant la machine ;

w : travail total reçu par 1kg de fluide en traversant la machine. Ce travail massique est une somme de trois termes :

1° : travail technique massique w' : travail fournie à 1kg de fluide par les parties mobiles de la machine ;

2° : travail moteur de la force de pression fourni par le fluide situé en amont de la machine : ;

3° : travail résistant exercé par le fluide situé en aval de la machine :

Si tu as du mal avec les termes 2 et 3 : revois la démonstration niveau (bac+1) sur la détente de Joule-Thomson. Cela conduit à l'expression du premier principe valide pour les systèmes ouverts :



L'enthalpie étant une fonction d'état, sa variation se calcule comme si le kilogramme de fluide traversait une succession de machines élémentaires fictives. Pour chaque machine élémentaire, la relation précédente devient :



La deuxième identité thermodynamique appliquée à chaque kilogramme de fluide s'écrit :



Si l'évolution est réversible : , donc par identification :

: ce travail technique massique réversible est souvent appelé travail massique de transvasement.

Dans le cas des turbines et des compresseurs, l'évolution est suffisamment rapide pour être considérée comme adiabatique ; si de plus, le fluide est assimilable à un gaz parfait, la seconde loi de Joule s'applique :



Si la compression ou la détente peut être considérée comme adiabatique réversible, le fluide étant assimilé à un gaz parfait, la loi de Laplace s'applique. Le taux de compression (ou de détente s'il s'agit d'une turbine) s'écrit :

d'où l'expression du travail massique de transvasement :



Quelques mots sur l'exergie maintenant. C'est une notion introduite pour caractériser la part utilisable d'une énergie donnée. Sa définition dépend donc du contexte expérimental. Je prends, comme dans ton message, le cas simple d'une source chaude de température Tc susceptible de fournir une quantité de chaleur Q pour obtenir une énergie utile : le travail W. Pour cela il faut imaginer un moteur thermodynamique fonctionnant entre cette source chaude et une source froide de température Tf (l'air ambiant par exemple). Le travail maximum récupérable est obtenue à l'aide d'une machine fonctionnant réversiblement entre ces deux sources. Le théorème de Carnot fournit le rendement d'une telle machine :



L'exergie est ainsi :



Tu trouveras d'autres renseignements ici :  

J'ai commis une étourderie de notation  après la phrase : "la seconde loi de Joule s'applique". Je rectifie :

Bonjour,

Merci pour vos explications et votre aide.

Je suis revenu à mon cours de thermodynamique (sup et spé) et j'ai bien révisé la partie où on applique le premier principe de la thermodynamique à un système ouvert (en réalité c'est un abus de language puisqu'on l'applique à un système fermé qu'on choisit).

Aucun problème pour les termes 2 et 3, merci !

J'ai trouvé du mal à suivre avec le site que vous avez cité, sûrement à cause des notations. Je pense que je vais laisser de côté la notion d'exergie pour l'instant afin de mieux structurer mes connaissances en thermodynamique et les consolider.

Après vos explications et ma révision du cours j'ai pu continuer dans le document en question (je lis ce document car j'aimerais faire des petites études de machines thermiques comme le réfrigérateur que j'ai chez moi...), je fus par contre bloqué par cette affirmation:

" Les irréversibilités (perte par frottement, dissipation visqueuse) sont assimilées à une source de chaleur interne . Comme la transformation est adiabatique, on a : "

J'ai suivi ce raisonnement afin de comprendre ce que l'auteur veut dire. Dans le cas d'une transformation irréversible, le deuxième principe s'écrit :
Cela me semble raisonnable de décomposer ainsi : . Une quantité de chaleur échangée par des processus thermiques (convection, rayonnement...) et une autre dûe à la cause de l'irréversibilité (frottements...). Comme la transformation est adiabatique, il est légitime de dire : .
Mais je ne vois pas pourquoi .
Une autre démarche serait de se dire que : (transformation adiabatique et ici c'est la chaleur échangée thermiquement) et de poser : . Mais je n'ai jamais vu ça lorsque je travaillais la thermodynamique. L'écriture : avait un certain sens où la température était celle échangée à la frontière du système. Mais si on écrivait : que serait cette température puisque ici la cause est l'irréversibilité.

J'ai une question qui m'est venu à l'esprit sans contexte précis. Je me souviens qu'on négligeait souvent l'énergie cinétique et l'énergie potentielle (massiques) dans le principe industriel lors des compressions, détente... Pour l'énergie potentielle c'est souvent le cas puisque l'écoulement du fluide se fait horizontalement. Je n'ai pas de mesures de vitesses entre deux transformations pour conclure sur l'énergie cinétique, mais dans le cas d'un turboréacteur par exemple, on a bien un compresseur à l'entrée, et on néglige la variation de l'énergie cinétique. Mais je ne sais pas si en réalité on peut faire approximation. (J'ai retrouvé dans mon cours un cas particulier du principe industriel où dans le cas des compresseurs... on néglige l'énergie cinétique et je me suis demandé si c'est pour tous les compresseurs).

J'espère que vous pourrez m'aider encore une fois afin de mieux comprendre et avancer.

Merci d'avance.

Il y a quelques erreurs dans ce que tu écris sur les transformations irréversibles. Même si ton niveau moyen dépasse largement celui du public moyen visé, tu pourrais peut-être jeté un coup d??il aux deux fiches que j'ai créées sur le premier et le second principe de la thermo. En particulier le paragraphe 3.4 sur les transformations quasi statiques sur la première fiche :
Premier principe de la thermodynamique
puis la définition de la réversibilité sur la seconde fiche :
Deuxième principe de la thermodynamique

Citation :
Dans le cas d'une transformation irréversible, le deuxième principe s'écrit :

Deux précisions.

Bonjour,
Je vous remercie pour vos réponses et votre aide. Les fiches que vous m'avez redirigé vers expliquent très bien les notions en question et permettent d'acquérir une certaine intuition.

J'ai aussi beaucoup apprécié la partie avec le coefficient polytropique car le choix du chemin est bien intéressant. J'ai continué les calculs au cas où une personne lit un jour ce sujet. J'ai trouvé :
J'aimerais vous demander une précision sur le chemin pris ici. Si le chemin est réversible et non adiabatique, ne serait elle pas plutôt la chaleur échangée thermiquement avec l'extérieur ? Vu que le chemin est réversible je doute qu'il y ait des frottements visqueux ou autre...
Je pense qu'il faudrait prendre un chemin où les pertes dues à la viscosité etc sont tolérées mais pas les pertes thermiques avec l'extérieur (convection...), mais dans ce cas le chemin ne serait pas réversible.

J'ai continué le texte pour voir comment l'auteur continue son étude des machines thermiques et j'ai trouvé qu'il continue de poser : .
J'ai compris la démonstration dans le cas réversible mais dans ce cas irréversible...

Je me demande s'il est raisonnable de continuer la lecture de ce document car à un instant l'auteur a défini le rendement polytropique de compression par : et affirme que ce rendement ne dépend pas de le taux de compression, alors qu'on a clairement :

Pourriez-vous me conseiller un document qui porte sur une étude thermodynamique des turboréacteurs s'il vous plait ? (avec tout ce qui est force de poussée...)
J'ai trouvé un document mais j'ai pas compris la formule qu'il développe pour la chambre de combustion :
Avec est la quantité de carburant (sans unité car c'est en kg de carburant par kg d'air) pour avoir une réaction totale (tout le carburant brûlé).   l'enthalpie de réaction à et la capacité thermique massique des gazs brûlés à la température de la chambre.

Ce qui me dérange dans cette formule, c'est que quand j'essaie de la prouver je trouve certaines inconsistances.
En utilisant le fait que l'enthalpie est une fonction d'état, on peut prendre un chemin où premièrement la réaction de combustion se fait à température constante puis le chemin où le système final est chauffé à la température
On a pour la première partie du chemin la variation d'enthalpie massique :

Sauf que puisque le texte donne on doit utiliser la loi de Kirchoff
Vu qu'il n'y a aucun changement d'état on peut utiliser l'approximation d'Ellingham, mais on n'a pas la réaction en question pour déterminer non ?

J'espère que vous pourrez m'aider encore une fois à travers cette aventure thermodynamique ^^

Merci d'avance

je crois qu'il y a une erreur de signe dans tes expressions de w'_pol et q_f . On peut ensuite les arranger un peu pour faire apparaître le rapport de compression et ainsi le rendement polytropique.



Loi des gaz parfait combinée à la relation de Mayer :





D'où la définition du rendement polytropique que tu rappelles. Puisque la fonction f telle que est monotone croissante pour x strictement positif, l'inégalité : }, une détente polytropique correspond à .

Le taux de compression est le rapport P2/P1 et non le rapport des températures. Les comparaisons entre les diverses compressions possibles : adiabatique réversible (fictive), adiabatique irréversible (réelle), modélisation polytropique (fictive) se font toujours pour un même taux de compression (P2/P1) ; c'est sans doute le sens, maladroitement exprimé, de la phrase de ton document sur le taux de compression.

La modélisation polytropique est réversible sans être adiabatique ; q_f est donc bien une quantité de chaleur massique reçue par le gaz. Cependant, même si les parois du compresseur ne sont pas correctement calorifugées, la compression est suffisamment rapide pour que les échanges thermiques avec l'extérieur soient d'importance négligeable. La chaleur reçue par le gaz est bien due aux irréversibilités : frottements divers...

Concernant la chambre de combustion d'un turboréacteur. La théorie est celle correspondant au calcul d'une température adiabatique de flamme, grand classique au niveau (bac+1) ! Ne pas confondre (c'est courant...) avec les lois de Kirchhoff sur l'influence de la température sur une enthalpie standard de réaction...
Voici un document sur les turboréacteurs ; je ne sais pas s'il correspond à tes attentes :

Bonjour,

Merci pour votre réponse. Effectivement j'ai commis une erreur dans le signe du travail polytropique et de l'énergie perdue par irréversibilité. Merci pour l'origine de l'expression du rendement polytropique. Cela me semblait tombé du ciel avant.
Je vois, pour un même taux de compression, on compare les différents chemins donc.

Excusez-moi, je ne comprends toujours pas l'origine de . Parce que si j'ai bien retenu les connaissances sur la réversibilité grâce à vos fiches, une transformation réversible est quasi-statique et renversable. On peut supposer que le chemin polytropique est quasi-statique (c'est un chemin fictif) mais si on autorise les pertes par frottements ... est-ce qu'on peut le supposer renversable aussi ?
Je trouve que si on laisse et en gardant les parois athermanes, alors on pourrait rajouter dans la transformation réelle (adiabatique et irréversible).

J'ai bien apprécié le document sur les turboréacteur. C'est concis, précis et complet je trouve. J'aurais préféré qu'il y ait des démonstrations de formules et peut être un rappel des notations utilisées, par exemple pour la chambre de combustion :

Bien qu'il explique ce qu'est et , je ne sais pas qu'est-ce ni . Pour moi G désigne l'enthalpie libre mais cela n'a aucun sens d'avoir une énergie au carré ici.

Pour la chambre de combustion, en notant la variation d'enthalpie pour le chemin isotherme à température de l'entrée de la chambre de combustion, où seule la réaction se passe, puis la variation d'enthalpie pour le chemin où on chauffe le système finale de à , température de sortie de la chambre de combustion. On a : , sauf qu'on n'a pas celle-ci dans les données mais . Je pense, pour pouvoir utiliser cette donnée, il faut supposer l'approximation d'Ellingham n'est-ce pas ?

Je vous prie de m'aider encore une fois et merci encore pour toutes vos explications et l'aide que vous fournissez.

Concernant la chambre de combustion : il s'agit d'utiliser une version simplifiée de la méthode d'obtention de la température adiabatique de flamme. Le "Ip" du document correspond à l'enthalpie standard de combustion, supposé indépendante de T (cf Ellingham) mais rapportée à un kilogramme de carburant, pas à une mole comme on fait en chimie. L'auteur considère le débit massique de carburant introduit très faible devant le débit massique d'air, noté G_air (ne me demande pas l'origine de ces notations bizarres) de sorte que la quantité de dioxygène réagissant est faible devant la quantité de dioxygène présente dans l'air , la combustion produit très peu de gaz de combustion (vapeur d'eau, CO2) de sorte que le mélange gazeux après combustion est toujours assimilable du point de vue thermodynamique à de l'air. En revanche, considérer la capacité thermique massique de l'air constante sur un intervalle de température aussi important est une grossière approximation.

La notation q_f peut effectivement être perturbante. Je reprends de façon simple (j'espère).
Évolution réelle irréversible et adiabatique : h=w'_irrev représente l'énergie mécanique réellement fournie au compresseur pour comprimer 1kg de gaz. Pour évaluer (il s'agit d'une estimation, d'une modélisation) l'importance de l'irréversibilité, on exprime le h réel par un chemin fictif réversible non adiabatique. Dans ce modèle, q_f est bien une quantité de chaleur massique fournie par le milieu extérieur et il en résulte un travail massique de compression w'_pol inférieur à w'_irrev. D'où la définition du rendement polytropique ; l'irréversibilité est d'autant plus importante que le rendement polytropique est faible et que qf est grand. On peut s'arrêter là dans la modélisation si tu préfères.

Bonjour,

Merci encore pour vos explications. Elles m'aident vraiment à avancer. Je ne sais pas si j'ai bien compris la modélisation polytropique, mais maintenant je la conçois comme ceci : les causes de l'irréversibilité se traduisent pratiquement par des pertes thermiques. Alors on va faire apparaître la conséquence de l'irréversibilité dans un terme de quantité de chaleur, et en faisant ainsi, on a un chemin "réversible" mais non "adiabatique" dans le sens où on a des pertes thermiques.  Je ne sais pas si c'est le fait que le chemin soit fictif qui nous permet de faire une telle "gymnastique". Parce qu'on pourrait se dire qu'on va toujours rajouter un terme de quantité de chaleur lié aux pertes par frottements...

Le fait qu'ils considèrent les produits comme de l'air m'a motivé pour redémontrer la formule mais comme je ne sais pas quel est mon problème avec les débits, j'ai toujours eu du mal avec. Je pense que j'ai cette idée que la thermodynamique est "statique dans le temps" qui entre en conflit avec l'idée que j'ai du débit qui "varie dans le temps".
J'ai essayé de faire certains calculs pour la chambre de combustion avec deux documents sur les turboréacteurs.

Le premier document est le votre et les hypothèses considérées sont : réaction non totale, réaction adiabatique, les produits c'est l'air (approximativement).
J'essaie d'utiliser ces hypothèses pour en arriver à l'équation présentée dans le document.
Réaction adiabatique et l'absence de parties mobiles permet de dire que :
Vu que l'enthalpie est une fonction d'état, on peut choisir un autre chemin pour trouver une expression exploitable de l'enthalpie.
Le chemin qu'on prend est composé de deux parties, la première (1) est à température constante d'entrée de la chambre de combustion et la réaction a lieu, la deuxième partie (2) est sans réaction mais échauffement à température .
Le système final étant de l'air on peut écrire :
Je ne vois pas comment passer de : à l'équation fournie par le document.  
Je comprends l'équation du document physiquement. Par conservation d'énergie, l'énergie de combustion d'une masse est égale à l'énergie de réchauffe de la masse des produits.
Mais je n'arrive pas à trouver comment avoir l'équation théoriquement.

J'ai fait un autre calcul, qui me semble plus rigoureux afin de retrouver la formule que j'ai évoqué avant :
Sachant qu'ici désigne la quantité (en Kg de carburant par Kg d'air) théoriquement nécessaire (si tout est brûlé) pour élever la température des gaz de la température d'entrée à la température de sortie .
Dans ce document, on a l'enthalpie massique de réaction qu'à 25°. Je suppose que puisqu'il la donne à cette température précisément c'est qu'il ne faudrait pas utiliser l'approximation d'Ellingham.
On va réchauffer l'air de la température de sortie du compresseur/ température d'entrée de la chambre de combustion à 298K, puis faire la réaction à 298K, et réchauffer le système final, qui maintenant sera de l'air et les produits de la réaction, à la température . Ce qui donne :

Ce qui donne après simplification :

Mais je ne vois pas comment faire apparaître des quantité de carburant, surtout telle qu'elle est définie ici.  

J'ai remarqué que dans les deux cas, c'est l'apparition d'un débit quelque part qui me pose problème. Probablement car je n'arrive à le voir qu'en tant que .

Je m'excuse, mon message est très long mais j'ai voulu insérer tout ce que j'ai fait et rencontré comme problème parce que par la même occasion ça me permet de réfléchir à ce que je fais.

J'espère que vous pourrez corriger encore une fois mes fautes de raisonnement et d'éclairer mes incompréhensions.

Merci d'avance.

Tu as bien compris je pense le phénomène à modéliser mais tu as effectivement un problème de compréhension au niveau des débits. Quelques mots de généralités à ce sujet. Dans le cas simple d'une entrée et d'une sortie, le régime permanent impose l'égalité du débit massique d'entrée et du débit massique de sortie, noté D_m. En multipliant par D_m l'expression classique du premier principe :



Le produit d'un débit massique par une énergie massique a la dimension d'une puissance. Pth est la puissance thermique reçue par le fluide, P' est la puissance technique, par exemple la puissance que doit fournir un moteur électrique à un compresseur pour le faire fonctionner. Cette formule se généralise facilement à une machine thermodynamique à plusieurs entrées - sorties :



Les débits sortants sont comptés positivement, les débits entrants négativement.

La chambre de combustion possède deux entrées : une entrée de carburant à la température T_c avec un débit massique D_mc, une entrée d'air à la température T₃ avec un débit massique D_ma. La chambre de combustion ne possède pas de parties mobiles : P'=0 ; aucun apport de chaleur de l'extérieur et évolution suffisamment rapide pour être considérée comme adiabatique : P_th=0 ; donc : . avec l'indice 4 pour les grandeurs de sortie :



où "g" désigne l'air qui n'a pas participé à la réaction et les gaz de combustion.

Puisqu'on raisonne sur des variations de fonction d'état, on peut modéliser la situation en envisageant les étapes suivantes :

- échauffement du carburant de T_c à T₃ : variation de puissance thermique :

- réaction de combustion à la température T₃ : variation de puissance thermique correspondante :

échauffement du gaz défini au dessus : variation de puissance thermique correspondante :

Finalement :



Cela donne une équation avec une inconnue T₄. On peut imaginer deux simplifications liées à D_mc<<D_ma : le premier terme concernant l'échauffement du carburant est d'influence négligeable ; le mélange air restant - gaz de combustion a sensiblement les propriétés thermodynamiques de l'air. On peut aussi utiliser l'approximation de Ellingham. Cela donne :



Cette formule est celle du document que je t'ai fourni.

En revanche : impossible, pour une variation aussi considérable de température, de considérer la capacité thermique massique isobare de l'air comme indépendante de T. On peu l'obtenir à partir des tables thermodynamiques en assimilant l'air à un mélange 80% de diazote, 20% de dioxygène (proportions molaires). Exemple de tables, ici, page 962 :

Bonjour,

Je vous remercie pour votre réponse. Je pense que je commence à mieux appréhender la notion de débit. J'ai toutefois deux questions qui me posent problème pour une bonne compréhension.

La première question porte sur la démonstration de la formule généralisée. J'ai essayé de la démontrer mais je ne sais si mes raisonnements sont corrects. On considère une machine avec i entrées et j sorties. Je vais faire le bilan thermique mais en ne tenant compte que d'une seule sortie. Je note l'enthalpie d'entrée du fluide venant de l'entrée _i et son enthalpie de sortie à la sortie j. On obtient pour ce fluide (après multiplication par son débit comme vous avez fait) :
Les deux puissances sont respectivement les puissance thermique et mécaniques fournies (algébriquement) au fluide _i. En sommant sur toutes les entrées :
Après un changement de notation et d'indice on peut écrire :
(avec les débits sortants comptés positivement et ceux entrants négativement).
Ici je ne traite que d'une seule sortie. Je ne sais pas si on peut sommer cette équation sur les sorties. Et aussi je n'ai pas traité de cas où l'un des fluides réagit avec un autre, où si un fluide ne sort que pas une seule entrée (par exemple si on l'utilisait pour refroidir la machine seulement).

La deuxième question est à propos de ce qui se passe quand on a une réaction entre deux fluides, comme dans notre chambre de combustion. En fait, dans la démonstration du principe industriel, on considère le régime permanent. Je ne sais même pas si c'est hypothèse reste vraie quand il y a une réaction. Car les particules à la sortie ne sont pas dans le même état énergétique que celles qui rentrent. Le seul moyen que je vois pour arriver à votre première équation : en réutilisant l'équation généralisée dans le cas de deux entrées et une sortie, c'est de supposer que l'enthalpie de sortie de l'air est égale à celle du carburant et c'est celle des gaz brûlés. Le problème ici est que le carburant a tellement diminué...  Ensuite, je ne comprends pas où se perd le pour qu'il ne soit pas dans l'équation finale et pourquoi alors qu'on a deux fluides qui réagissent entre eux, on ne considère l'enthalpie de réaction que dans l'enthalpie du carburant et non pas celle de l'air. Je trouve qu'elle devrait être dans les deux.
En fait, je comprends bien physiquement les deux équations, et je suis bien d'accord avec elles. Je pourrais presque la poser directement si quelqu'un me le demandait, le carburant qui est chauffé est à l'origine du premier terme, c'est lui qui régule le débit des produits puisque l'air est en excès, d'où le deuxième terme, et le troisième vient du réchauffement du système final (produit et air). Mais je ne comprends pas comment l'obtenir rigoureusement et les étapes à suivre.

J'aimerais vous poser une dernière question si vous me le permettez. C'est à propos de l'écriture de en fonction de la température. Ça me semble comme un développement limité. Si on se place à pression constante de sorte que , alors on peut dire qu'au voisinage d'une température on a : avec les constantes qu'on déterminera expérimentalement bien sûr. Le seul problème avec ça, c'est que ce n'est valable qu'au voisinage . Je me souviens qu'en thermodynamique statistique, on calculait la capacité calorifique pour un système à deux états et autres, mais je ne me souviens pas d'une telle formule.
Peut être c'est purement empirique aussi.

J'espère que vous pourrez m'assister dans cette démarche de comprendre la thermodynamique encore une fois.

Merci d'avance.

Les petits « delta » sont en trop : le produit d'un débit massique par une énergie massique est une puissance, pas une puissance élémentaire. Pour la démonstration, il suffit de considérer que la somme (P' +Pth) est, par unité de temps, la différence entre la somme des enthalpies entrantes et la somme des enthalpies sortantes.

Concernant la chambre de combustion, on peut parfaitement l'étudier en régime permanent. Loi de Lavoisier : la réaction de combustion change la composition chimique du gaz (très peu dans la mesure où Dmc<<Dma) mais ne change pas la masse. Le gaz sortant a donc comme débit massique : (Dma+Dmc).

Pour cp : tu parles de développement limité. Je parlerai plutôt de régression polynomiale. On réalise des mesures de cp à différentes températures puis un programme de régression calcule les coefficients du polynôme dont la représentation graphique passe au plus près des points expérimentaux.

Bonjour,

Je n'avais pas dû utiliser les , je voulais dire que était la puissance reçue par le fluide . Ça me dérangeait d'avoir mais maintenant que j'y pense, ça reste correct.

Vous avez bien raison, la masse se conserve. Je pensais à l'état énergétique mais c'était n'importe quoi.

Je vois pour . C'est une sorte de "polyfit" avec matlab ^^

J'ai réfléchi encore une fois à cette équation :

Mais je ne vois toujours pas pourquoi on perd ici :

Est-ce que ça se passe de la sorte :
On écrit d'abord :

et
Mais pour ? On doit quand même pourvoir y faire ressortir un terme lié à la réaction non ?

J'espère que vous pourrez m'aider afin de résoudre ce dernier mystère pour la chambre de combustion.

Merci d'avance.

Bonjour,

Merci beaucoup pour votre réponse.
Je pense que ce qui me posait problème aussi c'est de ne pas avoir bien compris l'hypothèse : . Je me disais qu'il fallait qu'on ait un terme dû à la réaction et qui relève de l'air et pas des carburants. Avec cette hypothèse on ne s'intéresse qu'à l'échauffement de l'air dans le système final et avec l'hypothèse que le système final est approximativement de l'air on peut mettre dans la deuxième loi de Joule au lieu de . Je pense que maintenant j'ai bien compris ^^ merci encore !

Une petite question, les températures qu'on utilise ici (et aussi la pression dans la loi des gaz parfaits, dans le taux de compression...) sont bien des grandeurs statiques et non d'arrêt n'est-ce pas ? Car je pense on regarde "ce qui est vraiment propre au gaz" et non pas ce qui est relevé par les capteurs.

Merci d'avance.

Bonjour,

Je m'excuse pour le double-post, mais je viens de travailler un exercice sur les compresseurs afin de mettre en pratique ce qui a été dit dans cette discussion et j'ai trouvé certains problèmes. Tout d'abord,  l'utilisations des grandeurs d'arrêts. Je ne sais pas si l'exercice est mal organisé en utilisant parfois l'appellation pression d'arrêt et parfois pression dynamique, mais il définit le taux de pression du compresseur par : (ici les deux pressions sont des pressions d'arrêt).
Ce qui me gêne, c'est que ce taux est constant, égal à selon l'énoncé, mais dans un tableau de données fournit, je trouve des valeurs variées.
Par exemple pour un ensemble de données, j'ai la pression dynamique d'entrée du compresseur : (en PSI) et la pression d'arrêt de sortie du compresseur : (en PSI), je rajoute donc car il est dit que le PSIG est en différentiel avec la pression atmosphérique (en PSI) et le taux de pression donne :
Ce qui est une valeur absurde comparée à celle fournie par l'énoncé. Je me demandais si le problème venait de moi, ou c'est vraiment une erreur dans les mesures, ou dans le taux fournit. Car si j'ai : , ce qui m'a l'air plus réaliste.

J'ai une autre question à propos du rendement isentropique. En fait, on sait que pour une transformation isentropique on a :
Ce qui donne :
Ça c'est pour une transformation isentropique.
Maintenant, quand on travaille avec une transformation non réversible, par exemple pour le compresseur, et on veut définir le rendement isentropique, on dit que :
Mais pourquoi on parle pas de
Pourquoi on suppose qu'il y a (ce que je trouve normal) et pas de .

Et surtout je ne comprends pas du tout, pourquoi on travaille avec des grandeurs d'arrêt. Est-ce que c'est comme pour l'optique ondulatoire où on travaille avec des moyennes parce que c'est ce que les détecteurs mesurent ? Et du coup tout ce qui est lié à la machine (taux de compression, rendement...) doit être calculé avec des grandeurs à l'arrêt ? Mais du coup pour le travail qui est calculé grâce au principe industriel et où on utilise la seconde loi de Joule pour la variation d'enthalpie, on fait comment ? Car je doute qu'on utilise des grandeurs d'arrêt pour ça.

J'espère que vous pourrez m'aider encore une fois dans cette nouvelle étape de compréhension.

Merci d'avance.

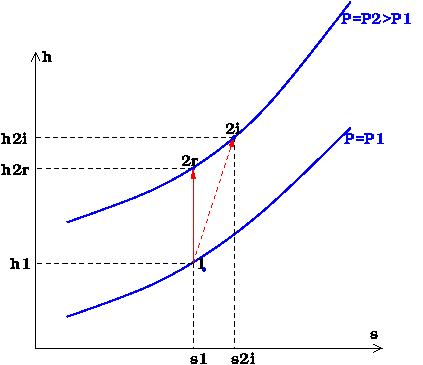
La notion de rendement isentropique est extrêmement utilisée. Pour bien comprendre, je trace les isobares P=P₁ et P=P₂ dans le diagramme enthalpique de Mollier (h,s). Partant d'un état 1 donné, une compression réversible adiabatique (isentropique) correspondrait à l'évolution 1-2 . Le travail massique de compression réversible est . La compression réelle est adiabatique et irréversible. L'entropie massique du fluide augmente donc. Pour un même taux de compression, la compression irréversible correspond à l'état de sortie 2i du diagramme. Le travail massique de compression irréversible est : . Pour un taux de compression donné, le rendement isentropique du compresseur est :



Bien sûr, l'irréversibilité rend le compresseur plus gourmand en énergie mécanique : ! Cela apparaît bien graphiquement.

Si le fluide peut être assimilé à un gaz parfait, la deuxième loi de Joule conduit à :



Bien sûr :



Comme déjà dit : les différentes compressions envisageables se comparent pour un même taux de compression et des valeurs identiques de P₂ et de P₁.

Pour tes questions sur les pressions : la plupart des manomètres indiquent la pression relative mais pas la pression d'arrêt ; les pressions prises en compte en thermo industrielle sont les pressions absolues du gaz. Certains auteurs assimilent la pression d'arrêt à la pression dynamique. C'est vrai dans pas mal de situations. Cela n'intervient pas en thermo industrielle sauf pour les tuyères et même là : c'est une notion dont on peu très bien se passer...

Bonjour,

Juste une remarque : la pression dynamique est parfois juste le terme d'énergie cinétique, ce qui justifierait la petite valeur de cette grandeur.

Bonjour,

Merci beaucoup pour votre réponse. C'est vrai que j'ai oublié qu'on garde le même taux de pression.
Donc puisqu'on travaille avec les pressions absolues, il est légitime de considérer que la pression d'entrée du compresseur est . J'ai un ensemble de différentes mesures de pression d'arrêt en sortie du compresseur en PSIG. Cet ensemble de valeur est : , je leur rajoute : pour avoir les pressions d'arrêt en PSI :
Pour avoir les pressions absolues à la sortie du compresseur il faudrait retrancher à ces pressions le terme d'énergie cinétique. J'ai bien les pressions dynamiques (en les considérant des énergies cinétiques) d'entrée correspondant à chaque point de fonctionnement, donc je peux avoir les vitesses d'entrée, mais je ne vois pas comment je pourrais avoir les vitesses de sortie. Tout cela en considérant bien sûr que la masse volumique reste constante.
Je me demande s'il y a une relation mécanique à appliquer pour avoir les vitesses de sortie en fonction de celles d'entrée. Mais même en cherchant sur internet je ne trouve que des études purement thermodynamiques pour les compresseur.
Peut être je me trompe aussi et qu'il faudrait regarder autrement pour calculer le taux de pression et ainsi le rendement isentropique.

J'espère que vous pourrez me guider encore une fois à travers ces études de machines thermiques.

Merci d'avance.

Le régime permanent, pour une machine avec une entrée et une sortie, implique un débit massique d'entrée égal au débit massique de sortie. ₁.S₁.V ₁=₂.S ₂.V₂.
Si le fluide est assimilable à un gaz parfait, si P et T  sont connues en entrée et en sortie, il est possible d'obtenir les masses volumiques qui ne sont pas egales.Si les aires des sections d'entrée et de sortie sont connues, on peut déterminer le rapport des vitesses d'écoulement.

Bonjour,

Une petite incursion et je m'éclipse.
Si on vous donne les grandeurs totales, faites les calculs en grandeurs totales, elles sont exactement les mêmes que pour les grandeurs statiques. En particulier, dans votre cas

Dans chaque domaine de la physique ayant des applications industrielles importantes, les « spécialistes » et les ingénieurs développent souvent un vocabulaire propre (variable d'un pays à un autre) et souvent utilisent des unités hors système international : tout cela complique singulièrement le travail de quelqu'un qui veut comprendre de façon approfondie sans nécessairement se spécialiser dans ce domaine. Il semble que ton document veuille prendre en compte les énergies cinétiques massiques d'écoulement. Cela peut se faire simplement, en utilisant les notations et les définitions de mes messages précédents, en reprenant ma démonstration du 15-05-20 à 14:39 et en ajoutant l'énergie cinétique massique :



V₂ et V₁ désignent les vitesses d'écoulement du fluide en sortie et en entrée de la machine.

Cela conduit à :



Ce qui peut se généraliser pour plusieurs entrées et sorties (voir message du 19-05-20 à 15:30) :



Je néglige toujours la variation d'énergie potentielle massique due aux éventuelles variations d'altitudes.

Reste bien sûr, que, pour les turbines et les compresseurs de gaz, la variation d'énergie cinétique massique est le plus souvent d'influence négligeable (voir message du 17-05-20 à 23:34).

Bonjour,

Merci pour vos réponses.

Je vois donc il faudrait faire les calculs avec les grandeurs totales. C'est vrai que j'ai trouvé ça un peu bizarre le système d'unités et surtout l'utilisations de grandeurs d'arrêt. Je m'étais dit que c'est peut être ce que relèvent les capteurs généralement mais comme vous m'avez dit que les capteurs mesurent généralement les grandeurs absolues, je ne vois pas d'explication à cela.

J'ai fait donc le calcul en grandeur totale. J'avais cet ensemble de valeurs de pressions d'arrêt en sortie du compresseur :
J'ai ces valeurs de pression dynamique en entrée du compresseur : , comme vous avez remarqué que ces probablement des énergies cinétiques, je rajoute , ce qui donne :
Je trouve ces valeurs pour les taux de pression :
Il y a quand même une assez grande différence entre ces valeurs, et surtout avec la valeur donnée .

J'ai aussi fait des calculs en grandeurs statiques. J'ai les valeurs des diamètres du moyeu d'entrée, du carter d'entrée et de sortie.
Je convertis déjà les pressions dynamiques d'entrée (qui sont des énergies cinétiques) en Pa :
Sachant que : , on peut obtenir les vitesses d'entrée au compresseur grâce
Ce qui donne : (en m/s)
Je note le diamètre du moyeu d'entrée et celui du carter d'entrée, on a
Avec et les valeurs : et on trouve les valeurs de vitesse de sortie : (en m/s) (c'est étonnant comment ces valeurs sont faibles)
Je convertis les pressions d'arrêt en sortie du compresseur en Pa :
Je retranche le terme , je trouve :

La pression statique en entrée étant : , j'ai ces valeurs pour le taux de pression :

Je n'ai toujours pas le même taux que celui du texte, mais ce qui est étonnant c'est que ces valeurs sont très proches de celles obtenues en grandeurs totales. Je ne sais pas théoriquement pourquoi, mais si (égalité des taux de pression), alors
Et on trouve que
Sachant qu'avec la compression, la pression augmente, on devrait avoir une vitesse de sortie plus grande que celle de l'entrée. Ce que je n'ai pas. Je me suis donc sûrement trompé dans la définition des surfaces. Mais ça reste étonnant que j'aie les mêmes taux de pression.

Je rappelle que le taux de pression ici est défini comme simple rapport de la pression de sortie sur celle de l'entrée.
Je me demande si c'est l'énoncé qui est en faute sur le taux de pression, mais cette différence entre les valeurs que j'obtiens reste un peu "flagrante" si j'ose dire.  Ce qui m'intrigue le plus c'est que j'ai clairement commis une faute dans le calcul des vitesses (puisque si on a le même taux alors les vitesses de sorties doivent être supérieures à celles d'entrée), et j'ai un résultat correct (selon gts2, ça revient au même de travailler avec des grandeurs totales ou statiques). Je sais que mathématiquement, le "faux" peut impliquer le "vrai", mais ça reste intriguant

J'espère que vous pourrez partager ce que vous en pensez.

Merci d'avance.

Bonjour,

En fait j'avais utilisé votre formule (conservation du débit massique) mais j'ai considéré que la masse volumique était constante.
Donc on a ces trois équations :
Et
Et la loi des gaz parfaits :
On pourrait donc écrire : mais je n'ai pas seulement d'arrêt.

Après avoir donné 36 noms à la pression (j'exagère bien sûr mais pas tant que cela !), tu te mets à distinguer deux températures, une statique et une dynamique. J'avoue que je n'y comprends plus rien ! La notion de point d'arrêt a, en dynamique des fluides, un sens très précis ; pour le reste... Sans parler que, après avoir relu tes différents messages depuis le 24 mai, je n'arrive pas à comprendre l'objectif de ton étude ! Je me demande si tu n'es pas en train de te compliquer la vie avec l'étude d'une thèse (archive HAL évoquée à ton premier message).
Si la pression n'est pas trop élevée pour que le gaz continue à pouvoir être assimilé à un gaz parfait, son volume massique et sa masse volumique vérifient :

Bonjour,

Veuillez m'excuser pour ma réponse tardive. J'avoue que je n'y comprenais plus rien aussi c'est pour cela que j'ai laissé de côté le sujet un petit moment pour y revenir avec l'esprit plus clair.

Pour l'objectif, c'est juste de travailler la thermodynamique. Le document de la thèse n'est pas si compliqué comme vous avez pu le constater c'est les mêmes notions de thermodynamique qu'en prépa et comme avoir des données sur des turboréacteurs est assez difficile, je me suis dit que c'est une bonne occasion de l'étudier en tant que machine thermique.

Au lieu de travailler avec 3 points de fonctionnements, je vais me concentrer sur un seul. Alors le but est de calculer le taux de pression.
Si on peut considérer que c'est le rapport des pressions d'arrêt, c'est clairement pas constant. Peut être une erreur de mesure.
S'il faut travailler avec les pressions statiques, alors il nous faut la vitesse à la sortie, puisqu'on n'a que la pression d'arrêt à la sortie.
Pour avoir la vitesse à la sortie on utilise la conservation du débit massique, ce qui nous donne :
On a la pression d'arrêt et la température d'arrêt à la sortie du compresseur, ce qui nous convient bien puisqu'on pourra utiliser la loi des gaz parfaits :
Ce qui nous donne :


Il reste à déterminer le produit
On a la relation de la pression dynamique à l'entrée :
En multipliant par la masse volumique on trouve :
On utilise la loi des gaz parfaits, mais puisqu'on a la température d'arrêt à l'entrée, on va rajouter la pression atmosphérique (qui correspond à la pression statique à l'entrée) ce qui donne :


On obtient à la fin la formule pour la vitesse à la sortie du compresseur :


Les données sont les suivantes : , , et
Le diamètre du moyeu d'entrée : et le diamètre du carter d'entrée :

Ce qui nous donne :

Je n'ai pas continué les calculs pour trouver la pression statique à la sortie du compresseur puisque cette vitesse m'a l'air très faible et donc qu'il y a une faute quelque part. Je suis sûr des formules obtenues, donc l'erreur se trouve soit au niveau des mesures, soit à l'utilisation des grandeurs d'arrêt (je suis sûr aussi des conversions d'unités). Je reprends la définition de point d'arrêt selon Wikipédia (c'est la même définition qui figure dans mon cours) : " Au point d'arrêt, la vitesse du fluide est nulle et toute l'énergie cinétique est transformée en énergie de pression de façon isentropique ". Donc si on travaille avec des pressions d'arrêt, c'est qu'on est en ce point d'arrêt et que la température qu'on considère doit être en ce point aussi. Mais je ne vois pas où est-ce qu'une erreur de l'utilisation des grandeurs d'arrêt peut être commise.

J'espère que vous pourrez me guider au cas où vous remarquerez quoi que ce soit d'inconsistant. Je cherche à déterminer le taux de compression car selon le document que vous m'avez envoyé " le compresseur est caractérisé par son taux de compression et son rendement isentropique ".

Merci d'avance.

Supposons donc que la « pression d'arrêt » soit la différence de pression mesurée par une sonde type « tube de Pitot », soit la différence entre la pression à l'extrémité du tube où la vitesse d'écoulement est nulle (point d'arrêt) et la pression du gaz. Cette « pression d'arrêt » est en fait l'énergie cinétique volumique macroscopique du gaz . Cela correspond bien à ton dernier message. Si tu fais le rapport entre la grandeur de sortie et la grandeur d'entrée (unité indifférente si tu utilises la même dans les deux cas) en tenant compte de la conservation du débit massique en régime permanent, tu obtiens :



Si les diamètres des canalisations sont connus, tu obtiens ainsi le rapport des vitesses d'écoulement.

Comme déjà dit :



La mesure de et la connaissance des paramètres d'entrée P₁ et T₁ permet la mesure de la vitesse d'entrée V₁. Connaissant le rapport des deux vitesses, tu obtiens celle de sortie. En supposant la compression adiabatique, la relation rappelée dans mon message du 26-05-20 à 11:10 conduit à :



mais il est fort probable que la variation d'énergie cinétique massique soit négligeable devant la variation d'enthalpie massique.

Juste une remarque :

Bonjour,

Merci pour votre réponse.

vanoise @ 29-05-2020 à 02:51


Comme déjà dit :

Pression statique, pression dynamique, pression motrice, pression d'arrêt, pression totale, tension... Ce vocabulaire spécifique, utilisé dans des domaines particuliers de la physique par des spécialistes de ces domaines... Je trouve cela plutôt gênant pour des étudiants généralistes et je préfère éviter ce vocabulaire, source de beaucoup d'ambiguïtés et d'incompréhension comme le prouvent les récents échanges  . Pour moi, comme déjà dit, désigne une énergie cinétique volumique, même si cette grandeur a la dimension d'une pression. Le taux de compression est le plus souvent défini comme le rapport (P2/P1). Le rapport que tu évoques est le rapport (T2/T1) dans le cas limite de la compression adiabatique réversible du gaz parfait.

L'expression de la masse volumique que je t'ai fournie est une application directe de l'équation d'état des gaz parfaits. La pression est tout simplement la pression du gaz.
Si tu étudies un turbo réacteur : attention : plus question de négliger la variation d'énergie cinétique massique devant la variation d'enthalpie massique au niveau de la tuyère.

Petit complément : ce que tu notes maintenant _c a été noté précédemment :

Bonjour,

Ah oui je m'excuse, le taux de compression était noté , merci de me le rappeler.

L'équation de Bernoulli (quand les hypothèses le permettent) : sur une ligne de courant

Je suis bien d'accord que le terme désigne une énergie cinétique volumique comme est l'énergie potentielle de pesanteur volumique et toutes les deux ont l'unité d'une pression. Sauf que dans notre cours on a appelé la première pression dynamique par opposition à la pression statique.

Je suppose que l'appellation de pression dynamique est sans intérêt. Je veux dire, on aurait pu appeler pression de pesanteur ou quelque chose comme ça mais ce ne sont pas de "vraies" pressions.

J'en conclus donc qu'il faut utiliser la pression statique pour le rapport de compression, la loi des gaz parfaits ...

Tu viens parfaitement de résumer mon avis mais c'est un avis de physicien et chimiste "généraliste". Certains chercheurs et certains ingénieurs, qui travaillent toujours dans le même domaine, finissent par développer un vocabulaire particulier qui leur fait gagner du temps dans leurs communications entre spécialistes mais qui n'est pas nécessaire lors d'une première approche, même approfondie.

Bonsoir à vous trois,

@EvDavid :

Citation :
Je suppose que l'appellation de pression dynamique est sans intérêt. Je veux dire, on aurait pu appeler pression de pesanteur ou quelque chose comme ça mais ce ne sont pas de "vraies" pressions.

Bonsoir,

gbm @ 31-05-2020 à 21:38


Et pourtant, je confirme ce que vanoise et gts2 ont pu t'écrire, c'est bien un terme qu'on retrouve dans le secteur énergétique, notamment dans la troisième filière industrielle du pays

Bonjour,

Oui c'est vrai, c'est juste que ça m'avait donner envie de refaire de la thermodynamique et quand j'ai vu turboréacteur dans l'un des documents, je me suis dit que c'est une bonne occasion de l'étudier aussi

Je pense que j'ai déjà  travaillé avec un diagramme de Mollier, mais ce n'était pas précis. Si je me souviens bien, on nous donnait des températures et pressions et on devait placer les points du cycle thermodynamique sur le diagramme. On ne raisonnait que par isotherme, isobare... et ce n'était pas des valeurs précises d'enthalpie que nous obtenions à la fin. Mais bon pour une utilisation personnelle c'est plus que suffisant.
Par contre, je n'ai jamais utilisé le logiciel Thermoptim. Peut être je vais y jeter un coup d'oeil, merci !

Bonjour à tous,

Citation :
Oui c'est vrai, c'est juste que ça m'avait donner envie de refaire de la thermodynamique et quand j'ai vu turboréacteur dans l'un des documents, je me suis dit que c'est une bonne occasion de l'étudier aussi

Bonsoir,

Ah oui, je n'avais pas remarqué que mon profil n'était pas à jour. Je l'ai remis à jour du coup.

Vous avez raison je devrais m'intéresser aux centrales thermiques aussi, surtout que tout ce qui est énergétique est d'actualité et concerne aussi le futur.

Merci pour tout !