Inscription / Connexion Nouveau Sujet
Que répondre?
Bonjour, je dois faire un DM pendant les vacances et j'ai un doute sur ce qu'il faut répondre à une question.
Il faut établir l'expression d'une énergie potentielle de pesanteur.
Est ce qu'il faut la calculer? ou bien juste écrire la formule?
Merci
Bonjour,
Etablir une expression c'est généralement la "calculer", la démontrer, la justifier... par un calcul littéral.
Mais il serait préférable que tu postes ton énoncé !
Voici l'énoncé (assez long):
Un pendule est constitué d'une petite bille de plomb, de masse m=65,0g , suspendue ç un fil inexitensible, de masse négligeabl. La bille, assimilée à un poin matériel, est distante d'une longueur l=1,00m du point fixe O où est accroché le fil.
Le fil du pendule étant initialement vertical, on l'écarte de cette position d'un angle de valeur 
m=60°.
Le fil étant tendu, on lâche la bille sasns vitesse depuis la position 1. Le pendule oscille alors dansun plan vertical. Les forces de frottements sont négligeables.
la question est donc : Pour une position intermédiaire, repérée par un angle de valeur que fait le fil avec la verticale, établie l'expression de l'énergie potentielle de pesanteur du pendule. (On prendra comme niveau de référence, la position la plus basse du centre d'inertie G de la bille)
Je n'arrive pas à trouver la distance de H vers H2 ... on peut trouver la distance de H1 vers H2 en faisant intervenir la trigonométrie, et je suppose que l'angle sert à quelque chose, mais je n'arrive pas à troouver sa valeur... de l'aide serai la bienvenue. Merci
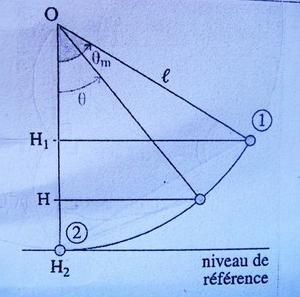
Que vaut OH2 (littéralement ! ) ?
Que vaut OP (j'appelle P le pendule) (toujours littéralement ! ) ?
Que vaut OH (toujours littéralement ! ) ?
OH2 et OP, c'est pas la même chose? et OH est bien ce que je cherche mais que je ne trouve pas. Je sais que OH2 vaut 1m mais littéralement... 
OH2 = l (la lettre l ; c'est ce qui est écrit sur la figure)
OP = l (évidemment ; rayons d'un même cercle)
OH... un tout petit peu de trigonométrie ! Tu connais OP = l et tu connais l'angle
Mais alors comment je peux déterminer la valeur de l'énergie potentielle de pesanteur si il me manque z dans Ep=m x g x z ??
z= cos ? donc cos 45°?
On ne te demande pas de calculer la valeur de l'énergie potentielle de pesanteur...
On te demande d'établir l'expression LITTÉRALE de cette énergie !
Tu n'as pas répondu à ma question de tout à l'heure... alors il sera difficile d'avancer !
Que vaut OH ?
Très bien ; mais tu te souviens que OP = l
Donc OH = l cos()
Tu sais aussi que OH2 = l
Que vaut H2H ?
Je n'aime pas le 1 ; on est en train d'établir une expression littérale il faut conserver des lettres
H2H = OH2 - OH = l - l cos() = l [1 - cos()]
d'accord, c'est comrpris. On me demande dans la deuxième question de calculer la variation d'énergie potentielle de pesanteur du pendule lorsqu'il passe de la position 1 à la position 2. Je trouve -0,319J, est ce que ce résultat semble correct?
Je suis incapable de passer à une question si la précédente n'est pas terminée.
Quelle est l'expression de l'énergie potentielle de pesanteur du pendule ?
Voilà, comme cela on peut avancer.
J'espère que tu as bien compris ce qu'est établir une expression littérale !
__________________
Oui, l'énergie potentielle de pesanteur diminue de la position 1 à la position 2
Tu peux compter négativement cette diminution dont la valeur numérique est bien -0,319 J
wa merci ! Alors l'inverse du travail du poids du pendule est égale à la variation de l'énergie potentielle de pesanteur donc on peut dire que le travail du poids du pendule est de 0,319J?
Exactement.
Le poids est la force qui transfère de l'énergie : diminution d'énergie potentielle en passant de 1 à 2 et simultanément augmentation de l'énergie cinétique. Puisque les frottements sont négligés l'énergie mécanique est constante.
Dans la question suivante on me demande quelle est la valeur de la vitesse v2 de la bille lorsque le pendule passe par la position 2? est ce qu'il faut utiliser l'énergie cinétique? parce que je vois pas d'autre lien entre la vitesse et l'énergie potentielle...
La vitesse à la position 1 est nulle.
Quelle est l'expression (littérale !) de l'énergie cinétique ? Cela te permettra de connaître la vitesse au passage à la position 2
On va voir cela.
1) l'énergie cinétique s'exprime en effet par Ec = (1/2)m.v2
2) La variation d'énergie cinétique entre une position 1 et une position 2 s'exprime donc par
Ec = (1/2).m.v22 - (1/2).m.v12
Or ici v1 = 0
Donc Ec = (1/2).m.v22
Tu connais Ec
tu connais m
il est facile d'en déduire v2
J'obtient 3,13m.S-1 avec les deux méthodes.
Si on avait eu autre chose qu'une bille de plomb (d'une autre masse) la vitesse aurait été modifié car l'énergie cinétique dépend de la masse, donc la vitesse aussi... c'est ça?
2) L'augmentation d'énergie cinétique (1/2).m.v2 provient de la diminution de l'énergie potentielle m.g.h
donc
(1/2)mv2 = mgh
v = 
(2gh)
Voilà pourquoi les deux méthodes donnent le même résultat !
Mais voilà aussi pourquoi la vitesse ne dépend pas de la masse
Avec une autre masse l'énergie cinétique aurait certes été modifiée mais la diminution de l'énergie potentielle de pesanteur aussi et ... la vitesse serait restée la même !
Nota bene : la valeur de 3,13 m.s-1 est correcte
Attention le symbole de seconde est s (s minuscule, pas s majuscule)
oui merci, c'était une erreur de frappe, c'est la fatigue ! Je vais dormir à présent. A très très très bientôt ! 
et surtout MERCI !
Annuler
connectez vous