Je comment déjà par définir le système d'étude : skieur + ski, le référentiel : terrestre supposé galiléen, et l'inventaire des forces : poids et la réaction de la piste.

Il faut ensuite que je développe ce qu'est le poids et la réaction.

1) Alors il me semble que dans les exercices que nous avons fait avec notre prof, nous n'avons jamais calculé de coordonnées, donc je suis un peu perdue sur la façon dont procéder. Je dirais qu'il faut que je parte du fait que Px = x et Py = y mais je ne suis pas sûre du tout car je pense qu'il faut utiliser P = 800N.

2)Je pense qu'il faudra que j'utilise certaines données trouvées avant et comme je ne les ai pas encore trouvée, je ne sais pas comment me dépatouiller avec cette question.

3) a) (il faudra que je fasse le schéma réduit à son centre d'inertie) Oui, le skieur peut descendre sans pousser sur ses bâtons.
   b) ext = donc f = -(P+Rn+Rt).

Je pense avoir beaucoup d'erreurs vu que je n'ai pas résolu la moitié de l'exercice... J'espère réellement que vous m'aiderez à mieux comprendre ! Merci.

Faut-il utiliser la trigonométrie pour la première question ?

oui il faut utiliser la trigo pour la première question et calculer la projection du vecteur P sur les axes x et y

Merci d'avoir répondu.

J'ai fais quelques recherches sur le net car je n'ai pas du tout compris le passage de la trigonométrie dans le cours. J'ai vu qu'il fallait faire :

Px = P sin et Py = P cos

Pourriez-vous m'aider à comprendre pourquoi s'il vous plaît ?

c'est presque ça. Tu as fait un dessin ?

Oui j'ai fais un dessin et c'est en train de beaucoup m'aider ! Mais je ne sais pas s'il est juste ><

J'ai essayé de faire une méthode, mon raisonnement est celui-ci :

On sait que + =
donc + {Rx}[/tex] = et + =
+ = et + =

Est-ce juste jusqu'à maintenant ? Car à partir de mon dessin, j'ai essayé de trouver ce que vaut et je ne trouve pas du tout, car mon vecteur part vers la droite. Je ne sais pas si vous voyez un peu près.

oui mais on en était à trouver Px et Py
c'est Px = P sin alpha  et Py = -P cos alpha
avec P = 800 N

ensuite on a bien ce que tu as marqué mais tu es toujours en vecteur donc fais maintenant des projections scalaires :
Px + Rt = 0 et Py + Rn = 0

D'accord, donc ce que j'ai mis ne résoud en rien ce que j'essaye de comprendre >< car je ne vois pas du tout pourquoi Px = P sin a et Py = -P cos a.

J'essaye à l'aide de mon dessin de comprendre mais j'ai vraiment du mal, de plus je fais beaucoup de recherches mais elles restent cependant infructueuses quasiment pour l'instant. J'ai beau retourner mon schéma dans tous les sens, je ne comprend pas.

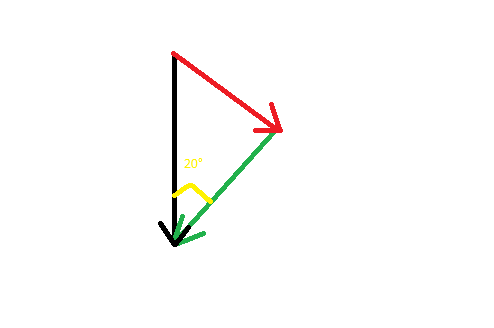
voilà le dessin

En noir on a P
en rouge Px et en vert Py
l'angle entre le rouge et le vert est droit. Il suffit de faire de la trigo. Les signes se déduisent de l'orientation des axes

Oh ! Merci beaucoup d'avoir pris la peine de faire ce dessin ! J'ai tout compris merci ! =)
En faite, tu as refais une représentation du vecteur P avec Px et Py en dehors du schéma, et moi j'essayais de le faire sur le schéma c'est pour ça que ça ne marchait pas >< Merci beaucoup !! =)

Par contre, j'essaye de comprendre pourquoi tu dis Py = -P cos a. Je suis désolée, je suis vraiment très nulle niveau force Est-ce une question de sens des vecteurs ? Ou, ah, je crois que je viens de comprendre : par rapport au schéma on a bougé le vecteur Py enfin... Non, je ne sais pas trop si c'est ça...

En attendant ta réponse je vais essayer de poursuivre mon raisonnement :

1)

Px = P sin et Py = P cos
Px = 800 sin 20 = 274 N et Py = 800 cos 20 = 752 N

Donc là on a les coordonnées.

2)


(Px-Rt) = (car le schéma indique que le vecteur i va dans le même sens que mon vecteur Px et mon vecteur Rt quand à lui est de sens opposé)
Px - Rt = 0

et


(-Py+Rn) = (car le schéma indique que le vecteur j va dans un sens opposé à Py mais dans le même sens que Rn)
-Py + Rn = 0

Ainsi : Px = Rt et Py = Rn
Donc Rn = 752
alors comme on sait que Rt = 0,2 Rn on a :
Px = 0,2 Rn = 150,4 ??? Ah bah non ça va pas vu ce que j'ai trouvé tout à l'heure ><

ba si c'est bien ce que tu as fait dans la 2

oui mais Px = 752 et Rn comme c'est égal à Py c'est égal à 274, on fait 0,2 274 = 150,4 qui n'est pas égal à Px (je me met des difficultés en plus ?? ><)

oula
on reprend :
Py = Rn mais Px Rt

Ah bon ? Pourtant j'ai noté que Px = Rt à cause des produits scalaires ?

ah oui pardon j'avais oublié de te corriger ça
le vitesse du skieur n'est pas constante donc il y a une accélération selon x !

Ah d'accord ! Donc lorsque la vitesse n'est pas constante, ce qui se trouve sur x ne se compense pas c'est bien ça ?

voilà

donc Rn = 752 et comme Rt = 0,2 Rn alors c'est bien égal à 150 !! Merci beaucoup ^^

de rien

3)
a)

Oui car le vecteur f est nul.

b)

_ext =

f = -(P + Rn + Rt)
f = -(800 + 752 + 150)
f = - 1702 N

J'espère que c'est la bonne réponse ! En tous cas, merci beaucoup pour ton aide car je ne savais vraiment plus du tout comment faire, de plus j'ai vraiment tout compris, tu m'enlèves une sacré épine du pied ^^ Bonne nuit et merci de ne pas m'avoir lâché en cours de route ! =)

le passage de la ligne 2 à 3 est bien entendu faux ^^ les vecteurs ne sont pas colinéaires. N'oublie pas le projections

Mince, je suis allée trop vite...


je ne vois pas trop comment faire là Les projections c'est bien avec les vecteurs i et j ? Je ne crois pas pouvoir mettre des vecteurs i et j ensemble... Je ne sais pas si tu vois ce que je veux dire.

=
-f - Rt = -P + Rn
-f = -P + Rt + Rn
f = P - Rt - Rn
f = 800 - 150 - 752
f = - 102 N

ça me paraît faux... J'ai du faire un erreur quelque part...

Je ne vois pas trop mon erreur

non ça ne va toujours pas ^^

tu ne peux pas mettre i et j ensemble effectivement

f = -(P + Rn + Rt) (le tout en vecteur)

ça fait :

-f = P sin(alpha) -Rt
et 0 = -Pcos(alpha) + Rn

Ah d'accord, mais j'essaye de comprendre pourquoi tu as rajouté des sin et des cos, est-ce que c'est pour remplacer les Rt ou Rn ?

non c'est Px et Py

Ah d'accord, merci ! mais ça veut dire que on n'a pas besoin de cette ligne là pour calculer f c'est ça  ? :

et 0 = -Pcos(alpha) + Rn

tu en as besoin pour connaitre Rn qui te donnera Rt

Mais j'ai déjà calculer Rn auparavant : Py = Rn = 752 N

oui on voit que la valeur est toujours la même ici

Ah d'accord, j'ai vraiment besoin de calculer Rn une seconde fois ? (enfin après je pense que c'est pour être sûre de la réponse c'est ça ?)

oui il faut recalculer mais c'est le meme calcul

D'accord, je te remerci pour toute l'aide que tu m'as apporté ! Grâce à toi j'ai pu terminer mon DM de physique en comprenant tout ce que je faisais !!

Merci beaucoup et bonne soirée à toi, bon nouvel ans !

de rien, tu feras beaucoup d'exo du même type en méca en 1ère et terminale

bon nouvel an à toi aussi