Inscription / Connexion Nouveau Sujet
Problème exercices Physique, formule littérale
On considère un pendule simple constitué d'une masse ponctuelle m attachée à l'extrémité d'un fil inextensible de longueur L et de masse négligeable. Le pendule est attaché à une de ses extrémité en O puis est écarté par rapport à la verticale d'un angle 0=60°
On lâche alors la masse m sans vitesse initiale. On considérera que l'énergie potentielle de pesanteur est nulle, lorsque le pendule se trouve à la verticale. Les frottements seront négligés.
1. Etablir la formule littéral donnant l'énergie potentielle de pesanteur de la masse m dans sa position initiale en fonction de m, L, g, et 0.
2. Comment varie l'énergie mécanique au cours de la descente de la masse ? Justifier.
3. En déduire l'expression de la vitesse de la masse à la verticale du point O.
4. Calculer cette vitesse dans le cas où L=3,2m. On prendra g=9,8 N/kg
Alors tout d'abord bonjour, voici l'énoncé d'un des exercices que je fais pendant les vacances, et j'avoue buté sur la 1 ère question (j'ai mis le reste en cas de besoin plus tard). La formule littérale initiale étant
Epp=m.g.z donc j'imagine bien que les deux premiers facteurs restes tels quels mais pour l'altitude du corps(z) je n'arrive tout simplement pas a trouver le lien possible qu'il peut y avoir avec L et 0 !
Si quelqu'un pouvait m'indiquer la voie cela m'aiderais beaucoup
Merci !
bonjour,
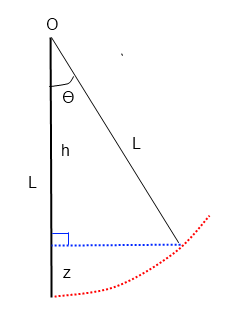
en faisant un dessin tu devrais trouver (cf ci-dessous):
on a:
L = h+z
et on connait h en fonction de L et de