Inscription / Connexion Nouveau Sujet
problème d'angle
Bonjour,
Qui pourrait m'expliquer ceci car pour moi le cos est une valeur sur l'axe des abscisses et le sin une valeur sur l'axe des ordonnées; pourquoi le vecteur vert qui est horizontal est-il dans un cas un cos et dans l'autre un sinus ?
Sinon pouvez-vous me dire dans quelle partie de la trigo il faut que je regarde ?
Merci
----------------------------------------------------------------------
si on considère une force F et un repère Oxy
F aura pour coordonnées le vecteur vert sur Ox et le vecteur bleu sur Oy dans le cas du 1er schéma
vecteur vert = F.cos a
vecteur bleu = F.sin a
Par contre, dans le cas du 2ème schéma
vecteur vert = F.sin a
vecteur bleu = F.cos a
ça dépend où est placé ton angle connu (ici a)
Bonjour,
Dans le triangle rectangle en B, ABC :
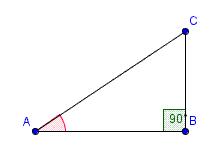
Sinus = côté opposé / hypoténuse
et
Cosinus = côté adjacent / hypoténuse

Bonjour,
je connais déjà CAH SOH TOA et ta réponse ne me pose pas de problème mais je n'arrive pas à faire le lien avec le 2ème cas : le vecteur vert est en dehors du triangle rectangle donc n'est ni un côté opposé ni un côté adjacent 
Pour ta deuxième figure, le vecteur vert est égal au vecteur que l'on pourrait construire entre les lettres y et F
Donc il est égal à un vecteur opposé à l'angle a
Il est donc égal à F  sin(a)
sin(a)

Lala, je pense que je commence à comprendre 
Est-ce que ce type de transposition est toujours autorisé et infaillible ou est-ce qu'il y a des exceptions ? Peux-tu me dire de quelle partie de la trigo cela fait partie ?
Merci
Il s'agit toujours de la trigonométrie (plane) dans les triangles rectangles.
La transposition est "infaillible" si tu dessines un rectangle. Ce qui est bien le cas ici. C'est souvent le cas en physique où l'on prend les parallèles et les perpendiculaires au support par exemple ; on dessine ainsi des rectangles et l'on a les diagonales de ces rectangles qui délimitent des triangles rectangles égaux. Il faut bien faire attention pour savoir quels sont les angles égaux dans ces triangles rectangles. Ensuite il est facile d'écrire des sinus et des cosinus.



