Bonsoir Maxwellx3,

voici une bonne adresse pour apprendre ce qu'est la pente d'une route . A la page 2 de ce document, tu trouveras en toutes lettres ce que veut dire "une pente de 5%".

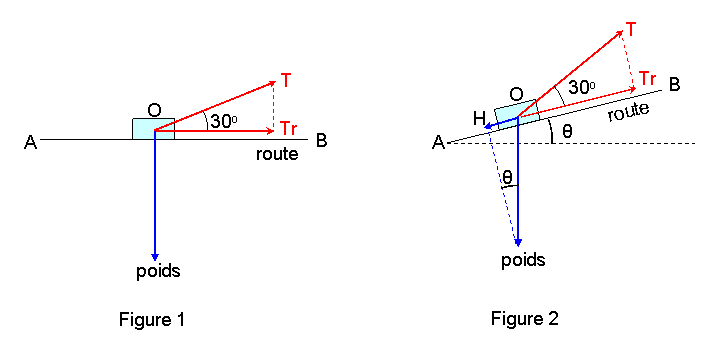
Maintenant, pour calculer le travail fourni pas la depanneuse, il faut projeter le poids de la voiture (qui est vertical) sur la direction du cable. Regarde la figure ci-dessous :

Sur la premiere, la route est horizontale ; le cable fait une angle de 30^o avec la route, donc un angle de 30^o avec l'horizontale. La projection du poids sur la direction du cable est OH, c'est contre elle que la depanneuse doit lutter pour tirer la voiture. Cette projection vaut mg.sin(30), ou m et la masse de la voiture, g = 9.8 m.s^-2 et sin(30) = 0.5. Le travail necessaire pour lutter contre cette force sur un deplacement d = 100 m est donc W1 = mg.sin(30).d. A toi de le calculer.

Sur la seconde figure, j'ai inclile la route de (theta) degres au-dessus de l'horozontale. Tu peux facilement voir que la projection OH du poids a auggente : elle vaut maintenant mg.sin(+30). Et donc le travail de la depanneuse a lui aussi augmente. Si tu sais calculer l'angle que fait la route avec l'horizontale (voir le s ite ci-dessus), tu n'auras aucun mal a termihner ton exercice.

Si tu as des questions ecris-moi.

Prbebo.

Bonjour Maxwellx3,

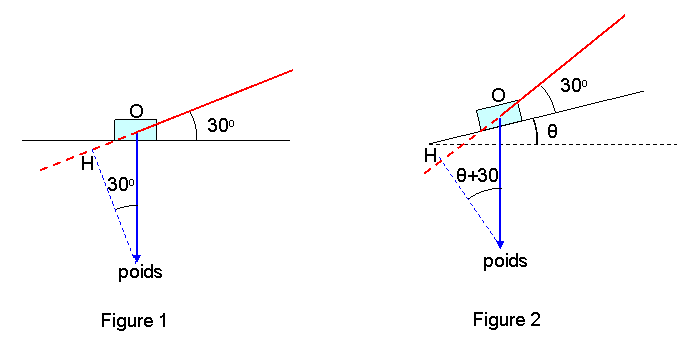
excuse-moi, mais je me suis trompe dans ma reponse d'hier soir. Retiens l'adresse du site qui explique ce qu'est la pente d'une route, mais oublie tout le reste, schema compris. On va reprendre ca calmement, avec le nouveau schema ci-dessous :

Sur la figure 1 j'ai represente la route horizontale, le chemin AB a parcourir (100 m), la tension T de la corde qui fait l'angle de 30 degres avec la route, et la projection Tr de cette tension sur la direction de la route. C'est cette projection qui est importante, car c'est elle qui va tirer la voiture vers l'avant. Or, dans le cas de la route horizontale le poids n'a aucune projection dans la direction de la route puisque sa direction est verticale. S'il n'y a pas de frottement, la projection Tr de la tension de la corde n'a aucune peine a tirer la voiture puisqu'elle ne lutte contre aucune force antagoniste : le travail depense pour aller de A vers B est donc nul.

Sur la figure 2, on retrouve les memes elements mais avec une route inclinee de l'angle de pente (le site que je t'ai indique donne tan = 5/100 = 0.05, soit = 2.86 degres). Cette fois la projection du poids sur la direction de la route n'est plus nulle : elle vaut OH = mg.sin, soit 416 N, et bien sur elle tire la voiture vers le bas de la pente. C'est contre cette force OH que doit lutter la depanneuse : pour qu'elle puisse tirer la voiture vers le haut, il faut que la projection Tr de la tension soit au moins egale a OH. Dans ces conditions le travail fourni pour faire le deplacement AB est W = OH.AB = 41600 Joules.

L'angle de 30 degres entre la corde et la route ne sert pas a grand chose. Eventuellement, si on te demandait de calculer la tension T de la corde, il faudrait partir de Tr = OH = 416 N. et diviser par cos(30^o). Tu peux aussi remarquer que cette tension T a une projection dans la direction perpendiculaire a la route. Cette projection va compenser la projection du poids dans cette direction, et donc de diminuer l'action du poids de la voiture sur la route (la voiture appuiera moins sur la route).

Voila, en te repondant hier soir j'avais en tete un exercice similaire et je me suis trompe. De nouvesu, toutes mes excuses.

A bientot, B.B..