Inscription / Connexion Nouveau Sujet
Problème avec calcul de forces résultantes
Salut ^^
Exercice 1 :
Trouver l'intervalle des valeurs de P pour lesquelles les câbles A et B restent bien tendus
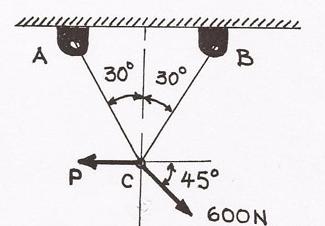
** énoncé effacé ; image laissée **
je ne suis pas sûre de la manière dont j'ai commencé à répondre à cet exercice, et après ce que j'ai fait je ne sais plus comment continnuer.
Il faut d'abord trouver les composants de chaque vecteur et puis faire la somme des forces en X et la somme des forces en Y et tout égaler à zero.
Puis on isole P de chaque écuation... et après je sais plus...
donnez moi un petit coup de main svp 
merci en avance.
Edit Coll : énoncé recopié
Edit Coll : à l'avenir, si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
Edit Coll : énoncé recopié
Edit Coll : à l'avenir, si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum
L'image c'est moi qui l'as desinné et j'ai traduit les instructions qui étaient en espagnol à coté, sauf que je l'ai mis sur l'image... mais bon, l'énnoncé de l'exercice est le suivant:
"Trouver l'intervalle des valeurs P pour lesquelles les tensions A et B restent bien tendues."
Merci.
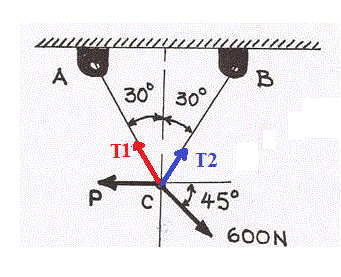
Projection sur un axe vertical :
T1.cos(30°) + T2.cos(30°) - 600.sin(45°) = 0
T1.(V3)/2 + T2.(V3)/2 - 600.(V2)/2 = 0
V3 T1 + V3 T2 - 600.V2 = 0
Projection sur un axe horizontal :
-P - T1.sin(30°) + T2.sin(30°) + 600.cos(45°) = 0
-P - T1/2 + T2/2 + 600.(V2)/2 = 0
-2P - T1 + T2 + 600.V2 = 0
On a donc le système :
V3 T1 + V3 T2 - 600.V2 = 0
-2P - T1 + T2 + 600.V2 = 0
T1 = 600.V2 + T2 - 2P
V3.(600.V2 + T2 - 2P) + V3.T2 - 600.V2 = 0
600.V6 + 2V3.T2 - 2V3.P = 600.V2
2V3.T2 = 600.V2 - 600.V6 + 2V3.P
Et pour que BC reste tendu, il faut T2 >= 0
Donc : 600.V2 - 600.V6 + 2V3.P >= 0
2V3.P >= 600V6 - 600V2
P >= (100V6 - 100.V2).V3
P >= 100.(3V2 - V6) N
T2 = T1 + 2P - 600V2
V3 T1 + V3.(T1 + 2P - 600V2) - 600.V2 = 0
2V3.T1 = 600V2 + 600V6 - 2V3.P
Et pour que AC reste tendu, il faut T1 >= 0
Donc : 600V2 + 600V6 - 2V3.P >= 0
2V3.P <= 600(V2+V6)
P <= 300(V2+V6)/V3
P <= 100(V6 + 3V2) N
Il faut donc :
100.(3V2 - V6) <= P <= 100(V6 + 3V2)
P en Newtons
-----
Recopier sans comprendre est inutile.
Sauf distraction.
Merci beaucoup J-P 
J'avais fait la somme des forces avec d'autres angles, mais à la fin je suis bien arrivée au même resultat:
Tx = T1cos(60°) + T2cos(60°) + 600cos(45°)=-P
Ty = T1sin(60°) + T2sin(60°) + 600sin(45°)= 0
Tx = 1/2 (T1-T2) + 300
2 = P [éq 1]
Ty = 3/2 + 3002 = 0 [éq 2]
puis j'ai isolé (T1-T2) en l'éq 2
vu que ces tensions doivent être égales alors la soustraction devais être la tension minimale et la reciproque la tension max
en sustituant (T1-T2) à la première éq. avec le signe moins original pour le min et puis en changeant le signe pour le max
alors en Newtons ca donne un peu près P=[179.315 ; 669.213]
merci encore J-P
Annuler
connectez vous