Inscription / Connexion Nouveau Sujet
prisme
slt
voici un exercice pour lequel je sollicite votre aide:
Un prisme de verre ABC rectangle isocèle, d’indice absolu n2, est posé sur le fond horizontal d’une cuve parallélépipédique dont les parois latérales sont verticales, transparentes et d’épaisseur négligeable. On remplit la cuve avec un liquide d’indice absolu n1 et on l’éclaire avec un faisceau cylindrique de lumière monochromatique perpendiculaire à la face d’entrée (voir figure).
1- Exprimer, en fonction de n2, la valeur maximale de n1 pour qu’il y ait un rayon réfracté en I dans le prisme.
2- Exprimer, de même, la valeur minimale de n1 pour que le rayon réfracté émerge en J par la face AC.
3- Les conditions précédentes étant satisfaites, exprimer, en fonction de n1 et n2 puis en fonction de n2 et de x=(n1/n2)^2 , l’angle de déviation δ d’un rayon entrant en H et sortant en K.
On supposera que le rayon sortant de la cuve émerge dans l’air d’indice absolu égal à 1.
4-L’expression de δ permet-elle de retrouver les conditions mentionnées aux questions 2.1 et 2.2 ?
Application numérique : n2=3/2 ; δ=30 °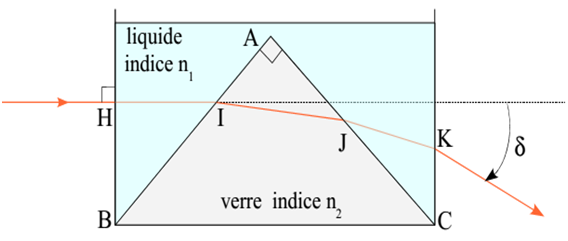
Edit Coll : mise en page

1)
i1 = 45°
n1.sin(i1) = n2.sin(r1)
sin(r1) = (n1/n2).sin(i1)
réfraction possible si : (n1/n2).sin(i1) < 1
n1 < n2/sin(i1)
n1 max = n2/sin(i1)
n1 max = n2/sin(45°)
n1 max = n2 * racine(2)
-----
2)
i2 = 90° - r1
n2.sin(i2) = n1.sin(r2)
n2.sin(90° - i1) = n1.sin(r2)
n2.cos(i1) = n1.sin(r2)
sin(r2) = (n2/n1).cos(i1)
sin(r2) = (n2/n1).Racinecarrée[1 - (n1/n2)².sin²(i1)]
sin(r2) = (1/n1).Racinecarrée[n2² - n1².sin²(i1)]
sin(r2) = (1/n1).Racinecarrée[n2² - n1².sin²(45)]
sin(r2) = (1/n1).Racinecarrée[n2² - n1²/2]
réfraction possible si : (1/n1).Racinecarrée[n2² - n1².sin²(i1)] < 1
(1/n1²).[n2² - n1².sin²(i1)] < 1
n2² - n1².sin²(i1) < n1²
n2² < n1².(1 + sin²(i1))
n1² > n2²/(1 + sin²(i1))
n1 > n2/Racinecarrée(1 + sin²(i1))
n1 min = n2/Racinecarrée(1 + sin²(i1))
n1 min = n2/Racinecarrée(1 + sin²(45°))
n1 min = n2/Racinecarrée(1 + (1/2))
n1 min = n2 * Racinecarrée(2/3)
-----
3)
90° - r2 + 135° + i3 = 180°
i3 = 180° - 138° - 90° + r2
i3 = r2 - 45°
n1.sin(i3) = n0.sin(r3)
avec n0 = 1 l'indice de réfraction de l'air.
sin(r3) = n1.sin(i3)
sin(r3) = n1.sin(r2 - 45°)
sin(r3) = n1.[sin(r2).cos(45°) + cos(r2).cos(45°)]
sin(r3) = (n1/racine(2)).(sin(r2) + cos(r2))
Or sin(r2) = (1/n1).Racinecarrée[n2² - n1²/2]
sin(r2) = (1/n1).Racinecarrée[(2n2² - n1²)/2]
cos²(r2) = 1 - (1/n1²).[n2² - n1²/2]
cos²(r2) = (2n1² - 2n2² + n1²)/(2n1²)
cos²(r2) = (3n1² - 2n2²)/(2n1²)
cos(r2) = (1/n1).Racine[(3n1² - 2n2²)/2]
sin(r3) = (n1/racine(2)).((1/n1).Racinecarrée[(2n2² - n1²)/2] + (1/n1).Racine[(3n1² - 2n2²)/2])
sin(r3) = (1/2).(Racinecarrée(2n2² - n1²) + Racine(3n1² - 2n2²))
r3 est l'angle delta.
delta = arsin[(1/2).(Racinecarrée(2n2² - n1²) + Racine(3n1² - 2n2²))
delta = arsin[(n1/2).(Racinecarrée(2(n2/n1)² - 1) + Racine(3 - 2(n2/n1)²))
et avec (n2/n1)² = x -->
delta = arsin[(n1/2).(Racinecarrée(2x - 1) + Racine(3 - 2x))
-----
4)
Pour que delta existe, il faut que les quantités sous le signe radical soit >= 0
---> x >= 1/2 et x <= 3/2
(n2/n1)² >= 1/2 et (n2/n1)² <= 3/2
n1 <= n2 * racine(2) et n1 >= n2 * racine(2/3)
On retrouve les conditions mentionnées aux questions 1 et 2
-----
Sauf distraction. 
Merci bcoup
mais j'ai une question comment est ce que delta est égal à r3
selon le schema c'est pas le cas!!!!
je propose;
delta=(i1-r1)+(r2-i2)+(r3-i3)
mais j'ai une question comment est ce que delta est égal à r3
selon le schema c'est pas le cas!!!!
Ben si, c'est le cas.

delta est l'angle en orange sur le dessin du haut
r3 est l'angle en vert sur le dessin du bas.
Ces angles ont leurs cotés directement parallèles 2 à 2 ... et sont donc égaux.



