Inscription / Connexion Nouveau Sujet
Planter un poteau - variation d'énergie potentielle.
bonjour,
j'ai des difficultés pour répondre à plusieurs questions de ce cet exercice.
Pouvez vous m'aider ?
Nicolas veut planter un poteau de basket dans son jardin. Le poteau sera assimilé à un cylindre homogène de longueur L = 4,0 m et de diamètre d = 9,0 cm. La masse du poteau est M = 18 kg. Le poteau est posé sur le sol horizontal, puis est dressé verticalement et enfoncé dans le sol sur une profondeur l = 60 cm.
a) Calculer la variation de l'énergie potentielle du poteau entre le début et la fin de l'opération.
b) Réaliser un diagramme pour représenter les échanges d'énergie pendant l'opération
c) Quel est le travail des forces autres que le poids exercées sur le poteau au cours de l'opération ?
Ce que j'ai fait :
a)
Ep = -
= mg(
-
.
) = 3,40 m
= 0,09 m
donc Ep = mg(3,40 - 0,09) = 584,48 J
b) c'est bon pour cette question
c) il y a la réaction et la force de frottement
comme
est verticale, son travail est nul. Je ne sais pas pour
.
Pouvez vous m'aider et me dire si ce que j'ai fait est faux ?
Merci d'avance.
Re - bonjour,
A quelle hauteur se trouve le centre de gravité du poteau :
. quand le poteau est posé sur le sol horizontal (que l'on prend pour origine dans les calculs de variation de l'énergie potentielle de pesanteur) ?
. quand le poteau est planté (dressé et enfoncé de 60 cm) ?
Le poteau est assimilé à un cylindre homogène donc quand il est couché, son centre de gravité est à une hauteur de 4,5 cm donc = 0,045 m
Lorsqu'il est planté il se trouve à 2,20m donc = 2,20 m
donc Ep = mg( -
) = 396,42 J
Est-ce correct ?
Je comprends mieux ce 1,70 m... mais ce n'est pas cela.
Une fois le poteau planté (et donc enfoncé de 60 cm en terre) à quelle hauteur du sol se trouve son centre de gravité (qui ne bouge pas... horizontal ou vertical, planté ou non, le centre de gravité est toujours au même endroit) ?
le centre de gravité se trouve à 2 m de hauteur lorsque le poteau et planté.
Je trouve cette fois Ep = 361,11 J
La centre de gravité du poteau se trouve toujours à 2 mètres de chacune des extrémités du poteau ; toujours au milieu du poteau.
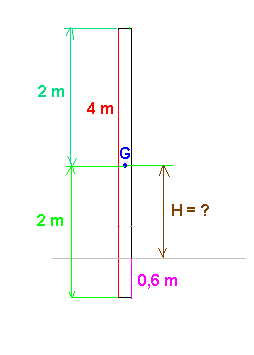
Quand le poteau est debout, enfoncé de 0,60 m dans la terre, à quel hauteur au-dessus du sol se trouve le centre de gravité ?
Merci de répondre à cette question avant de calculer l'énergie.
Oui, la hauteur du centre de gravité au-dessus du sol vaut bien 1,40 mètres une fois le poteau planté.
Quel calcul fais-tu pour trouver la variation de l'énergie potentielle de pesanteur du poteau entre le début et la fin de cette opération ?
Ep = Ep(B) - Ep(A) = mg( -
) = mg(1,40 - O,O45) = (176,58)(1,35) = 239,26 J
Autant pour moi je m'étais encore trompé.
On y arrive 
Essaie de comprendre pourquoi tu te trompes ; je te dis cela très sincèrement et en espérant que si tu comprends pourquoi tu pourras très rapidement progresser.
tu m'a beaucoup aidé pour cet exercice
Annuler
connectez vous