Inscription / Connexion Nouveau Sujet
Physique
Coucou !
On considère un support plan incliné d'un angle 
=20.0° par rapport à l'horizontale. L'extrémité d'un ressort de raideur k=12.5N.m^-1 est fixé au support, tandis qu'à l'autre est accroché un palet autoporteur de masse m=410g g de centre d'inertie G. Le ressort est parrallèle au support.
Un petit compresseur placé dans le palet envoie un jet d'air par un orifice situé au centre de la semelle du palet, afin de générer un coussin d'air entre le palet et le support. Soit vect(R) la force exercée par le coussin d'air sur le palet. Quand l'ensemble est immobile, le ressort est alongé de 
L=110mm. On prendra g=9.81N.kg^-1 pour l'intensité de la pesanteur au lieu de l'expérience.
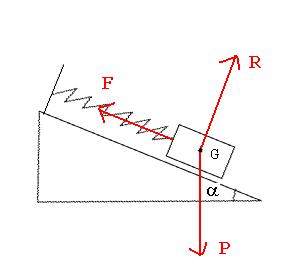
1. Reproduire le schéma. Représenter la force de rappel vect(F) exercée par le ressort sur le palet. Calculer F.
2. Même question pour le poids vect(P) du palet.
3. Le palet étant immobile, indiquer en la justifiant la relation vectorielle vérifée par vect(R), vect(F) et vect(P).
4. Calculer les composantes normales et tangentielles de vect(R)en utilisant des projections sur les axes de la relation trouvée à la question précédente. Ajouter la force vect(R) sur le schéma.
5. Expliquer en conclusion le rôle du coussin d'air.
Mes gros problèmes viennent du schéma parce que g du mal à comprendre l'expliquation du haut, donc forcément les autres questions je ne les trouve pas.
salut,
voici un schéma de ton problème
Les formules des forces P et F sont dans ton cours
Pour la projection des vecteurs, utilise comme axes, une droite suivant le plan incliné et une droite perpendiculaire.
Si je ne me trompe pas, tu devrais obtenir une force R sera bien perpendiculaire au plan incliné, donc suivant l'axe y si tu prends les axes que je te conseille.
Bon courage
Sylv'
J'ai regardé la réponse postée et voilà ce que j'ai fait :
F = k * L
F = 12.5 * 110.10-3
F = 1.375 N
P = mg
P = 410.10^-1 * 9.81
P = 4.022 N
D'après le principe de l'inertie, le palet étant immobile, le vecteur vitesse 
(G) du centre d'inertie ne varie pas, la somme des forces s'exercant sur le solide est donc nulle.
vect(P) + vect(R) + vect(F) = vect(0)
Je projette la relation sur l'axe oy :
vect(P) + vect(R) + vect(F) = vect(0)
-P * cos + R + 0 = 0
R = p * cos
R = 4.022 * cos20
R = 3.779 N
Je ne crois pas que ce soit juste parce que je n'arrive pas par ces résultats à déduire le rôle du coussin d'air.
Aidez moi svp
re-salut...
en regardant de plus prêt, je pense que l'exercice doit être interprété aurtement.
Je me suis un peu trompé
en fait, on ne te dit pas que la force R est perpendiculaire au plan incliné. Je l'ai un peu déduit rapidement, mais c'est assez logique dans l'ensemble, ce sera juste ta conclusion finale.
En fait :
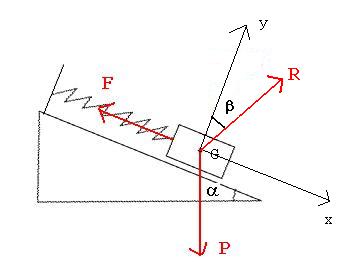
de façon plus rigoureuse, il faut prendre le schéma suivant :
en projetant tu en déduis :
Rcos(
)=Pcos()
Rsin()+Psin()=F
Tu peux calculer en remplcant R (tu obtiendras tan()=...)
tu pouuras déduite =0
ou alors directement, en mettant les deux relations au carré, tu auras cos²+sin²=1 et tu auras R²=?
dans tous les cas, tu retombes sur ta valeur de R calculé auparavant, et =0
Tu en déduis que R est perpendiculaire à la pente, et donc, son travail est nul.
Conclusion, l'air sert à ce qu'il n'y ait pas de frottement entre le plan incliné et la masse...
S'agit-il du principe de l'inertie ? Et dans ce cas, la relation que j'ai trouvé est-elle juste ou pas ?
De plus, comment fait-on pour calculer Rn et Rt en projettant sur les axes la relation ?
salut,
Oui on peu appliquer le principe d'inertie comme tu l'as fait
Ta relation était bonne dans le cas où le vecteur R était suivant (Gy). Or je m'étais un peu trompé, à savoir, que l'énoncé ne disait pas que cette force R était perpendiculaire au mouvement. Je l'avais supposé, alors que c'était la conclusion que l'on voulait que tu trouves
Il faut donc que tu refasses ce que tu as fait, avec un vecteur R quelconque, comme je l'ai dessiné sur la dernière figure.
En projetant la relation vectorielle que tu as trouvé sur les deux axes (Gy) et (Gx), tu obtiens deux équations avec R et comme inconnus (ou Rn et Rt)
Par résolution tu devrais obtenir que Rt=0 et Rn=3.779 N
D'où comme auparavant R=3.779 N et =0
J'ai eu exactement le meme exercice a faire mais j'ai beau y mettre toute ma volonté je ne parvient pas à résoudre la question 4 !! Vous pouvez m'aider s'il vous plait ?
Annuler
connectez vous