Inscription / Connexion Nouveau Sujet
physique
Bonjour, j'ai commencé à faire cet exercice mais je n'arrive pas à le finir... Le voici :
On étudie un modèle réduit fait d'un solide de masse m=100g accroché à un élastique. La première partie de la chute du solide est libre, puis l'élastique se tend et agit. On enregistre l'énergie cinétique Ec du solide, l'énergie potentielle de pensanteur Epp du solide, l'énergie emmagasinée par l'élastique U et la somme des trois Em. On prend g=10N/kg
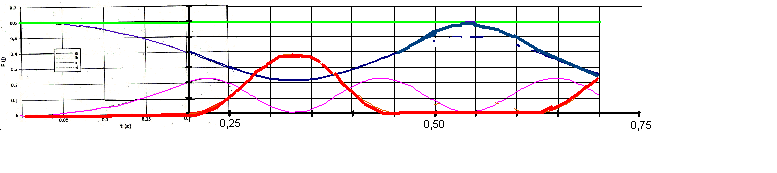
a)Identifier chaque courbe
b)Justifier le fait que le solide est lâché sans vitesse initiale
c)déterminer la durée de la phase en chute libre et la profondeur de chute qui correspond
ce que j'ai fait:
a)
a->Em
b->Epp
c->Ec
d->U
sauf que je croyais que l'énergie mécanique était la somme que de Epp et Ec.. (?)
b)U devient non nulle après environ t=21s. A ce moment Epp vaut environ 0,37J donc a diminué de 0,23J. L'altitude a donc diminué de 0,23m (mg=1,0N).
Lisez vous la même chose déjà? Ensuite trouvez vous pareil?
c)Reproduire les courbes et continuer de les dessiner jusqu'à t=2sec
Comment savoir à quoi elles ressembleront jusqu'à t=2sec?
Merci
a) OK
b) L'énergie cinétique du solide est Ec(t) = (1/2).m.(v(t))²
Comme le graphe montre que Ec(0) = 0, c'est que v(0) = 0 --> le solide est lâché sans vitesse initiale.
c)
La chute est libre tant que l'élastique n'a emmagaziné aaucune énergie, donc pour t dans [0 ; 0,2] s
La variation de l'énergie potentielle de pesanteur du solide entre les instant t=0s et t=2s est de -0,2 J
Et donc mg.delta h = -0,2
delta h = -0,2/(mg) = -0,2/(0,1*10) = -0,2 m
La hauteur de chute libre est donc de 0,2 m.
-----
Delta Ep entre t = 0,2 et 0,25 s : -0,1 J
-0,1 = mg. delta h --> delta h = -0,1/(0,1*10) = -0,1 m
L'énergie emmagasinée dans l'élastique pour un allongement de 0,1 m est de 0,11 J (lu sur le graphe)
--> avec k la constante élastique de l'élastique, on a: 0,11 = k * 0,1²/2
k = 22 N/m
La période de l'oscillation sera donc : T = 2Pi.racinecarrée(m/k) = 2Pi.racinecarrée(0,1/22) = 0,42 s (pulsation de l'oscillation : x = 2Pi/T = 14,8 rad/s)
Par établissement de l'équation différentielle régissant le mouvement d'oscillation, on arrive à ceci :
avec x l'allongement de l'élastique, on trouve:
mg - kx = m.d²x/dt² -->
d²x/dt² + 220x = 10
Et en tenant compte des conditions initiales et quelques développements on arrive à ceci :
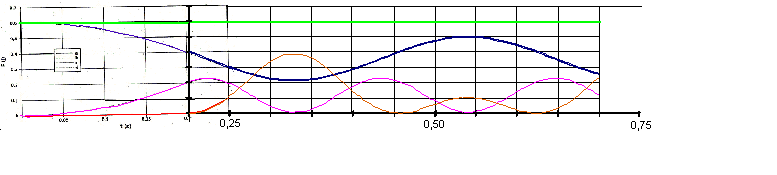
L'oscillation continue de la même manière puisqu'on ne tient pas compte des pertes qui amortiraient le mouvement...
Je doute qu'on puisse trouver ces courbes avec les connaissances acquises en 1ère... mais c'est peut être possible.
"No Se" en Espagnol.
Sauf distraction. 

Bonsoir,
j'ai tout mélangé dans l'énoncé:
a)Identifier chaque courbe
b)Justifier le fait que le solide est lâché sans vitesse initiale
c)déterminer la durée de la phase en chute libre et la profondeur de chute qui correspond
d)Reproduire les courbes et continuer de les dessiner jusqu'à t=2sec
a)Ok mais reste mon interrogation "sauf que je croyais que l'énergie mécanique était la somme que de Epp et Ec.. (?)"
b)Ok
c)Je ne comprends pas ce que entends par "variation d'Epp", négative en plus.. sinon j'ai capté.
Mais ma réponse était juste non?On tombe sur la même chose. Peut être trop précise ?
d)Je ne comprends pas grand chose, surtout à la fin. D'après toi en 1ère ce n'est pas faisable..
d)en fait l'énoncé était en anglais, j'avais un peu mal traduit: je dois juste dessiner leur allure en justifiant (mais rien de précis) 
a)Ok mais reste mon interrogation "sauf que je croyais que l'énergie mécanique était la somme que de Epp et Ec.. (?)"
Em = Ec + Epp est vrai si on ne considère que la pesanteur.
Mais il existe d'autres formes d'énergie potentielle que celle due à la pesanteur.
Dans le cas de l'exercice : un élastique étendu possède aussi de l'énergie potentielle.
Et donc on a ici :
Em = Ec + Epp + Epe
Avec Epe l'énergie potentielle élastique de l'élastique.
Et on a : Epe = k.x²/2 avec k la constante d'élasticité de l'élastique et x étant l'allongement de l'élastique (à ne pas confondre avec la longueur).
Dans le cas d'un élastique, x ne peut pas être < 0 (on ne peut pas "comprimer un élastique, alors qu'on peut le faire avec certains ressorts).
Donc, dans le cas de l'élastique:
Epe = k.x²/2 si x >=0

Je saisi. 
Masterrr et moi rencontrons un problème ici : https://www.ilephysique.net/sujet-chimie-volume-equivalent-237671.html
Si tu pouvais nous dire ce qui cloche 
Sinon ça ne fait rien.
Dernière chose J-P, si je dois juste dessine l'allure des courbes sans calcul jusqu'à t=2s, comment expliquer que la courbe orange sur ton graphique "ne remonte pas toujours à la même hauteur"? Même question pour la courbe bleue.. 
Pourquoi l'allure de la coube rouge est-elle celle que j'ai dessinée ?
Et aussi pourquoi n'est ce pas "tout à fait" correct ?
a)
L'allongement de l'élastique est de la forme : Allongement(t) = A + B.sin(wt) avec A et B des constantes.
L'énergie potentielle de l'élastique est donnée par Ep(t) = (1/2).k.[Allongement(t)]²
Et donc Ep(t) = (1/2).k.[A + B.sin(wt)]² = (1/2).k.[A² + B².sin²(wt) + 2AB.sin(wt)]
La présence dans cette relation du terme en sin²(wt) et du terme en sin(wt), donne la forme dessinée en rouge.
-----
b)
Pourquoi n'est ce pas "tout à fait" correct ?
Parce que l'élastique n'est pas l'équivalent d'un ressort.
Un ressort peut être à la fois étiré et comprimé, alors q'un élastique peut être étiré mais pas comprimé.
Dit autrement, la force d'un ressort est F = -k.x avec (x l'allongement du ressort, mais x peut être aussi bien > 0 (ressort étendu) que < 0 (ressort comprimé).
Pour un élastique, on a F = -k.x (x l'allongement de l'élastique), mais ceci n'est vrai que si x > 0.
Si x < 0, alors on a un élastique non tendu mais ne communiquant aucune force à la masse attachée à une de ses extrémité.
La courbe rouge du dessin a été donnée comme si on avait un ressort à la place de l'élastique.
Si on a vraiment un élastique, lorsque la masse remonte et arrive au point où l'élastique n'est plus tendu, la vitesse de la masse est non nulle et est vers le haut. La masse va donc se comporter comme étant en chute libre avec vitesse initiale vers le haut (et donc uniquement soumise à la pesanteur) jusqu'à ce qu'elle redescende et recommence à tendre l'élastique à nouveau.
Tout cela est abordable par le calcul (il me semble l'avoir déjà fait sur ce site (ou sur un autre ?)) mais ce n'est pas
franchement abordable en 1ère.
Cela va déformer localement toutes les courbes (bleue, mauve et rouge).
Notamment, la courbe rouge va rester à 0 au lieu de remonter avec les bosses de plus faible valeur.
Mais cela modifie aussi un peu les autres courbes, et cela devient assez difficile à dessiner sans calculs.

Ouch je n'ai pas toutes les notions pour comprends la totalité de ton explication.
Ce que je voudrais c'est juste expliquer par une phrase sans calcul, l'évolution de chaque courbe, sauf que à part "ben ça se sent" j'y arrive moyen.
Après si c'est impossible,ou compliqué, ou si ça commence à faire long pour cet exo pour toi je comprendrais 
L'énergie potentielle de pesanteur diminue puis réaugmente en valeur car l'objet a une altitude qui varie.
L'énergie cinétique diminue puis réaugmente car la vitesse de l'objet change "en bas" et "en haut" la vitesse est moins élevée.
Ce n'est pas très bien expliqué.
Par contre pour Em et U 'énergie emmagasinée par l'élastique)....