Bonjour,

1) La charge q de masse m située au point M subit trois forces:

- une force de Coulomb répulsive dans la direction AM venant de la charge q en A

- une force de Coulomb répulsive dans la direction BM venant de la charge q en B

- son poids, dans la direction verticale, vers le bas.


2) Les 2 forces de Coulomb ont la même amplitude puisque les charges en A et B sont identiques et que les distances AM et BM sont égales.

Lorsqu'on les décomposent sur un axe vertical et un axe horizontal, on a donc:

- les 2 forces d'amplitude identique sur l'axe horizontal se compensent, donc s'annulent.

- les 2 forces d'amplitude identique sur l'axe vertical s'ajoutent et s'opposent au poids de la masse m de l'objet mobile placé au point M.

L'objet sera immobilisé si la somme des amplitudes des 2 forces de Coulomb projetées sur l'axe vertical sont exactement égales à l'amplitude du poids.

3) Pour que la masse m s'éloigne de la position d'équilibre et des charges en A et B, il faut réduire la masse m pour que le poids soit plus petit que la somme des 2 forces de Coulomb.

La nouvelle masse m' < m va s'élever et devrait se mettre à osciller autour de la position d'équilibre correspondant à la distance du segment AB valable pour la masse m'.

Bon courage

PS: Je te laisse chercher pour les expressions exactes qui font appel à la géométrie et aux cosinus/sinus/tangente

merci beaucoup Revelli. Je vais bien regarder et si j'ai des questions je te les poserais. merci encore

je n'arrive pas à déterminer m ...

Bonsoir,

Le poids vaut P=mg

Soit la valeur des 2 angles égaux du triangle isocèle.

Soit l la distance MA=MB, d la distance AB et a la distance du point M à la droite AB.

D'après Pythagore, on a l²=a²+d²  

La projection verticale des forces de Coulomb vaut
F_AM[sub]V[/sub]=F_AM[sub]V[/sub]=k*q²*sin/l²

avec sin=a/l=a/(a²+d²)

d'où mg = (2*k*q²*a)/[(a²+d²)*(a²+d²)]

càd mg = (2*k*q²*a)/(a²+d²)^3/2

Soit m= (2*k*q²*a)/[g*(a²+d²)^3/2]

A toi de vérifier

Bonne fin d'année

Que veut dire F AM_V=F AM_V

enfin les [sub] ??

Je vais vérifier, mais toi, es-tu sûr de ce que tu as écrit ?

Et la 3/, comment faut-il modifier la masse m pour que M s'éloigne des charges A et B avec un mouvement rectiligne accéléré ?

je marque ce que tu m'as écrit càd : Pour que la masse m s'éloigne de la position d'équilibre et des charges en A et B, il faut réduire la masse m pour que le poids soit plus petit que la somme des 2 forces de Coulomb.

La nouvelle masse m' < m va s'élever et devrait se mettre à osciller autour de la position d'équilibre correspondant à la distance du segment AB valable pour la masse m'.


merci
et bonne année 2008

1)


-----
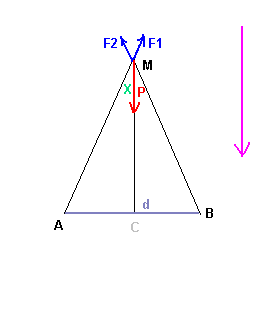
2)

Soit X l'angle AMC
MC = a
AC = d/2

|F1| = 9.10^9 * q²/AM²

AM² = MC² + AC²
AM² = a² + (d²/4)

|F1| = 9.10^9 * q² / (a² + (d²/4))

De la même manière:
|F2| = 9.10^9 * q² / (a² + (d²/4))
---

Projection des forces sur un axe vertical:

P - F1.cos(X) - F2.cos(X) = 0
P - (F1+F2).cos(X)  = 0
P - 2*[9.10^9 * q² / (a² + (d²/4))].cos(X)  = 0
mg = 2*[9.10^9 * q² / (a² + (d²/4))].cos(X)
m = 2*[9.10^9 * q² / (g.(a² + (d²/4)))].cos(X)

Or MC = AM.cos(X)
cos(X) = MC/AM = a/V(a² + (d²/4)) (Avec V pour racine carrée)

m = 2*[9.10^9 * q² / (g.(a² + (d²/4)))] * a/V(a² + (d²/4))

m = 18.10^9 * a . q² /[g * (a² + (d²/4))^(3/2)]
-----
3)
Il faut diminuer m
-----
Sauf distraction.  

merci beaucoup J-P (Correcteur)

Je ne vais pas recopier bêtement, je vais essayé de tout comprendre bien sûr.
Merci encore et bonne année 2008

Bonjour,

J'ai actuellement cet exercice à faire pour mardi.
J'ai réussi la première question, et j'ai regardé l'explication pour la question 2, j'ai essayé de suivre le calcul de J-P. Je comprends sauf le cos(X) et la projection avec les axes me pose un souci, où doit-on les placer sur le schéma ? Est-ce que quelqu'un peut m'aider s'il vous plait ?

Merci d'avance.