Inscription / Connexion Nouveau Sujet
perception de profondeur avec l'oeil humain
Bonjour,
Je suis nouveau sur forum mais j'ai pu voir que vous apportez des réponses interessantes.
voilà ma question, ou plutot mon probleme :
Imaginons une route de 6 mètres de large à quelle distance l'oeil humain confond-il les 2 bords de cette route?
Merci d'avance pour votre aide précieuse.
Bonjour,
Je te donne une réponse très approximative, parce que les bords d'une route ne sont pas des objets optiquement définis, contrastés, etc.
Si l'on considère que la limite de résolution d'un œil pour deux traits est atteinte quand l'angle entre ces traits vaut 1'
Alors on trouverait pour deux traits distants de 6 mètres une distance de l'ordre de 20 kilomètres.
Je ne suis guère satisfait de cette réponse mais je n'ai rien de mieux à t'offrir. Peut-être quelqu'un d'autre aura-t-il une réponse mieux fondée.
Ah ça tu devrais savoir le faire...
À quelle distance deux points distants de 6 m sont-ils vus sous un angle d'une minute (1') ? (on suppose la ligne qui joint les deux points perpendiculaire à la ligne de visée)
Simple problème de diamètre apparent.
Étonnant... de nombreux exercices en seconde traitent du diamètre apparent.
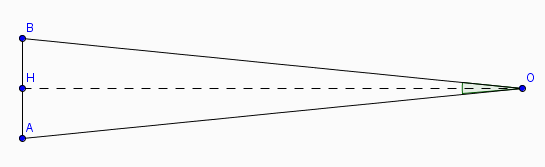
AB = 6 m
Quelle doit être la longueur OH pour que l'angle ait pour mesure 1' ?
Bonjour à tous,
J'ai le même problème que titit007 !
Je vais suivre la figure de Coll (voir ci-dessus) pour être clair.
Suivant les données que Coll a apporté (que l'angle BOA vaut 1' d'arc)
J'ai converti cette donné en degrès (c'est a dire 1,67*10^(-2)°)
puis j'ai calculé :
HB=3m
BDH = 1,67*10^(-2)/2 = 0,84*10^(-2)
Puis j'ai fais appel à la trigonométrie notamment à la tangente !
tan(0,84*10^(-2))=3/x
tan(0,84*10^(-2))x=3
x=3/tan(0,84*10^(-2))
x=6,2m
Cependant je trouve mon résultat totalement incohérent ou me susi je trompé ?
Bonjour,
Je suis d'accord avec x = 3 / tan(0,008 33...)
À la condition de ne pas oublier que 0,008 33 est la mesure de l'angle en degrés
Ou bien, avec la calculatrice paramétré pour les angles en degrés :
tan(0,008 33...) 
0,000 145 44
Ou bien, conversion de l'angle des degrés en radians
0,008 33° = 0,008 33 
/ 180 0,000 145 44 rad
et pour les petits angles (c'est vraiment le cas ! ) on assimile la tangente de l'angle exprimé en radian avec la mesure de ce même angle en radian
et donc tan(0,008 33°) tan(0,000 145 44 rad) 0,000 145 44
Si bien que x 3 / 0,000 145 44 20 600 m ou 20 km
D'accord ?
Cette réponse est completement fausse !!
D'apres la correction du prof il faut utiliser thales.
je vous laisse trouver la suite !
notre professeur nous a dit que notre démonstration basée a partir des reponse est completement fausse !
ne pas se fier !
Annuler
connectez vous