Inscription / Connexion Nouveau Sujet
Pendule simple et énergie cinétique
Bonjour !
Je bute un peu pour commencer ce problème de physique sur l'énergie cinétique, si quelqu'un pourrait me dire par où commencer cela m'aiderait bien.
(Je joins un petit schéma explicatif)
Voici l'énoncé :
Un pendule simple est constitué d'une petite bille assimilable à un point matériel, de masse m=50g, attachée à un fil inextensible de longueur l=40cm.
L'ensemble est fixé en un point O et on considère que les forces de frottements sont négligeables.
1. On écarte le pendule de sa position d'équilibre d'un angle 
0=40° (position A de la bille).
On le lâche sans vitesse initiale. On repère la position du pendule par la valeur de l'angle que fait le fil avec la verticale. Calculer le travail des forces de pesanteur lorsque l'angle que fait le fil avec la verticale passe de la valeur 0 à la valeur .
Je sais que pour calculer le travail du poids W(P)=mgh ou -mgh mais ici le travail est un travail moteur donc W(P)=mgh. h est la longueur de l'altitude du point de départ moins celle du point d'arrivée, or ici je ne sait pas du tout m'y prendre pour calculer cette valeur de h.
Merci d'avance
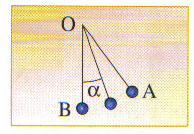
Utilises la figure. Arrives-tu à voir que lorsque l'on projette le vecteur reliant O à la masse sur un axe vertical (OB par exemple) on trouve une composante verticale égale à ?
On a donc pour :
et pour un point quelconque:
D'où le travail entre les deux positions:
Ou la ou la.
Peux-tu m'expliquer ? Je sais qu'il faut projeter mais la je ne vois pas où.
Si j'ai bien compris on doit calculer le travail de P en l'instant ou il est en A et celui ou il est dans la position intermédiaire entre A et B c'est ça ?
Mais merci d'avoir répondu 
Je remonte car je ne comprends pas d'où sort le "-lcos".
Pouvez-vous détailler ? Car pourquoi MOINS l ? Le poids ici n'est-il pas un travail moteur donc pas de moins ?
Je suis vraiment perdue.
Je viens de comprendre la projection ! Ton message m'a bien aidé donaldos merci !
Néanmoins je ne suis pas d'accord avec ton "-lcos", car dans ce mouvement la bille descend, donc le poids effectue un travail moteur (comme je l'ai dit plus haut), car ici 0°
90° (car 40°); ainsi on a lcos. Il est facile de le vérifier avec des calculs trigonométriques.
Ainsi le travail du poids devient : W(P)=mg(za-zb)=mgl(cos-cos0)
En revanche, la question suivante me pose un léger souci :
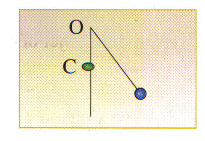
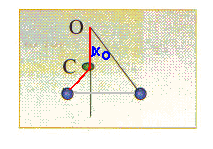
2. On recommence l'expérience en plaçant une butée en C. Le point C est sur la verticale passant par O, à 12 cm en dessous de O. A quelle hauteur remonte la bille ? Conclure.
Comment dois-je partir ?
Merci d'avance
po13po,
Il n'y a pas de différence entre le travail du poids donné par donaldos et le tien.
-----
2)
Conservation de l'énergie mécanique de la bille -->
La bille remontera à la même altitude que celle qu'elle avait au départ.
Merci de ta réponse J-P.
Le problème est que je n'ai pas vu l'énergie mécanique, seulement la cinétique. Comment puis-je m'en débrouiller ?
Et ainsi, tu comprends ?
Energie cinétique au départ + travail du poids sur le trajet = énergie cinétique à l'arrivée
Or dans les positions décrites, la bille est à vitesse nulle dans la position de départ et dans la position d'arrivée -->
Energie cinétique au départ = 0 et énergie cinétique à l'arrivée = 0 -->
0 + travail du poids sur le trajet = 0
travail du poids sur le trajet = 0
Or travail du poids sur le trajet = mg*(altitude de la bille au départ - altitude de la bille à l'arrivée)
Et donc : mg*(altitude de la bille au départ - altitude de la bille à l'arrivée) = 0
--> (altitude de la bille au départ - altitude de la bille à l'arrivée) = 0
altitude de la bille au départ = altitude de la bille à l'arrivée
-----
Bonjour,
J'ai le même type d'exercice à faire mais je dois déterminer la valeur v de la vitesse de la petite sphère au passage par la position d'équilibre, les frottements étant négligés.
Je suppose que je dois utiliser le théorème de l'énergie cinétique, mais je ne sais pas comment l'utiliser. Je suis perdu :s
Quelqu'un pourrait m'aider s'il vous plait?
Annuler
connectez vous