Inscription / Connexion Nouveau Sujet
Pendule et énergie
Bonjour voici un exercice en dm baccalauréal D, juin 2002 amérique du sud que je n'arrive pas à faire:
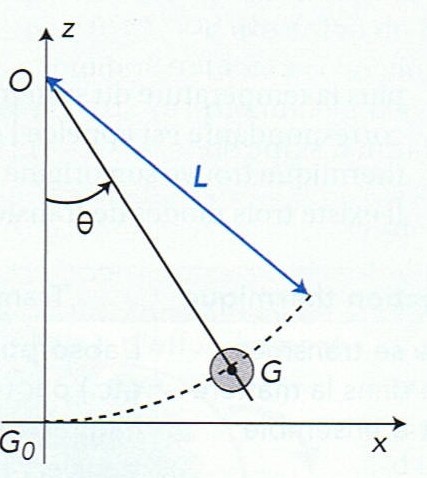
Le mouvement d'un pendule a été filmé. Le traitement avec un logiciel de pointage vidéo a permis d'obtenir les courbes ci après. Ce pendule est constitué d'une bille de masse m=30g suspendue à l'extrémité d'un fil inextensible de masse négligeable. L'autre extrémité du fil est accrochée est un point O fixe dans le référentiel terrestre. Le repère (G0,x,z) est représenté ci-contre. L'altitude de G0 est prise pour référence des énergies potentielles de pesanteur.
a) Rappeler l'expression de l'énergie cinétique du pendule et celle de l'énergie potentielle de pesanteur du pendule en fonction de z.
b) Pour quel angle 
l'énergie potentielle de pesanteur du pendule est elle nulle ?
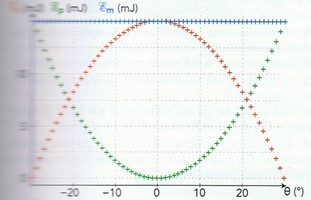
c) D'après les courbes, comment varie l'énergie mécnique du système ? Que peut on en conclure sur les forces de frottement de l'air exercées sur la bille ?
d) Quelle est l'énergie cinétique maximale du pendule ? En déduire la valeur de la vitesse maximale du pendule.
e) Calculer la hauteur maximale atteinte par le pendule.
j'ai fait :
a) Ec=1/2m.v² et Epp=m.g.z
b) pour =-30°C et 30°C
pour les autres je ne sais pas merci
Yo,
c'est la même méthode que j'ai pu t'expliquer dans les autres exercices.
Par ailleurs, il s'agit d'interpréter les courbes ce qui est à ta portée.
Au travail 
ok 
donc :
a) Ec=1/2mv² et Epp=m.g.z
b) pour =-30° et 30°
c) d'après les courbes, l'énergie mécanique du système est constante donc les forces de frottement sont...
d) l'énergie cinétique maximale du pendule est de 15MJ. Ec=1/2mv² donc v=31622.7m/s
e) ?
Donc,
a. OUI TB !
b. NON ! Regarde les graphiques !
Epp est maximale pour ces angles.
Elle est nulle à l'altitude z = 0 donc pour un angle nul.
c. Donc les forces de frottement sont négligeables puisque le mouvement est conservatif.
d. ATTENTION ! On parle de mJ et non de MJ !
b. Oui, c'est ça
d. Le raisonnement est bon. Je te fais confiance pour l'application numérique.
e. Tu connais la valeur de l'angle et tu veux h connaissant la longueur du pendule.
Une fois de plus, si tu utilises le schéma, ne vois-tu pas une petite relation de trigonométrie qui pourrait te permettre d'arriver à tes fins ?
J'appelle H la projection orthogonale de G sur l'axe (Oz) :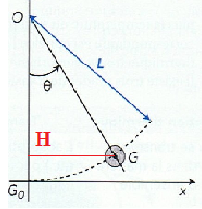
Soit z = GoH
z = OGo - OH
avec
OGo = L
OH = Lcos
d'où z = L(1-cos)
3 / 2
Annuler
connectez vous