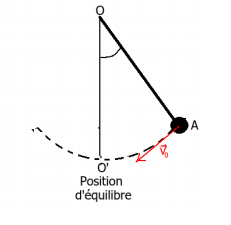
salut ,aidez moi s'il vous plait a résoudre cet exercice:Un pendule est formé d'une tige rédige OA,
de longueur l = 50cm, de masse négligeable
et d'un corps ponctuel placé en A de masse
m=200 g .
On écarte le pendule d'un angle α = 30◦
par rapport à sa position d'équilibre stable
et on le lance avec une vitesse initiale −→V
orthogonale à la droite (OA) .
Les
frottement sont négligeable . On prend l'état de référence pour l'énergie potentielle de pesanteur
le plan horizontal qui passe par O' et l'axe
−→
O′
z orienté vers le haut .
On donne g = 10N/kg
1. Déterminer la valeur minimale de v0 pour que le pendule puisse effectue un tour complet:
2. Sachant qu'on le lance avec une vitesse v0 = 4, 5m/s , déterminer les valeurs minimales
et maximales de la vitesse du corps et son énergie cinétique .

j'ai appliqué la conservation de l'energie mécanique au point ou la pendule est écarté et a la verticale de la position d'équilibre c.a.d z=2l
Em0=Em1
2)j'ai pris v min pour epp max cad z=2l et v max pour epp min cad z=l(1-cos(alpha))
merci pour tout aide.