Inscription / Connexion Nouveau Sujet
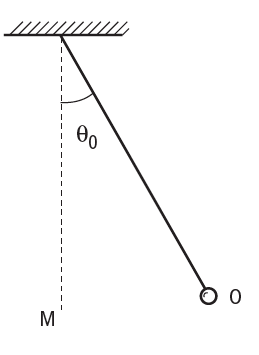
Pendule
Une petite sphère métallique, de masse m, est suspendue à l'extrémité d'un fil inextensible de masse négligeable et de longueur l. Le fil est accroché par son autre extrémité en un point fixe. On écarte le pendule de la verticale d'un angle sans vitesse initiale.
Données:
1. Exprimer l'énergie potentielle de pesanteur de la bille lorsque le pendule est lâché d'un angle en fonction de m, g, l et (on prendra comme position de référence la position M).
- Calculer sa valeur.
2. Exprimer le travail du poids fonction de m, g, l et
lorsque la bille passe de O en M. Calculer sa valeur.
3. Comparer le travail du poids et la variation d'énergie potentielle de pesanteur de la bille lorsqu'elle passe de O en M.
4. En déduire la variation d'énergie cinétique de la bille lorsqu'elle passe de O en M.
MES RÉPONSES:
1.
2.
3. Variation d'
La variation d'énergie potentielle de pesanteur de la bille lorsqu'elle passe de O en M est égale à l'opposé du travail du poids
4. Dans mon cours j'ai trouvé cette formule:
mais je ne sais pas quoi en tirer.
Merci de m'aider.
Bonjour,
Je pars de ta réponse à la question 3
Cette réponse est tout à fait correcte.
Maintenant je regarde les deux applications numériques des questions 1 et 2 :
6,2 J pour la question 1
6.10-3 J pour la question 2
Or, je pense que tu es d'accord si je te dis que tu aurais dû trouver la même valeur, d'après le résultat de la question 3 !
Alors, recommence les "deux" applications numériques pour les questions 1 et 2 (je te signale que les deux résultats que tu annonces sont faux tous les deux).

Effectivement, j'aurais pu vérifier.
Donc je recommence:
Apparemment c'est toujours faux mais ne vois pas où est l'erreur.
Ta calculette travaille en radians et non pas en degrés. Voilà d'où vient l'erreur !
. Ou bien
Paramètre ta calculette pour les degrés
. Ou bien
ne touche pas au paramétrage de ta calculette, mais transforme 25° en radian
Le genre d'erreur à éviter au bac ! 

J'ai pensé à ça moi aussi et ai dait un reset puis j'ai verfié avec Google et cos 25 fait bien 0,99...
Eh non !
cos(25 rad)  0,991 203 ...
0,991 203 ...
cos(25°)  0,906 308 ...
0,906 308 ...
Si je te dis que c'est de là que vient l'erreur, c'est que je l'ai vérifié 

Ah okay, je ne savais pas que Google aussi était en radians.
Problème réglé.
E_pp = 0,07J
W = 0,07J
Bon?
L'unité "officielle" pour la mesure des angles est le radian. Mais le degré a encore de beaux jours devant lui.
C'est cela ; mais l'arrondi est un peu "violent" quand même. Tu aurais pu garder deux chiffres significatifs.

La relation que tu as trouvée dans ton cours est correcte.
Que vaut (1/2)mVO2 et pourquoi ?
Que vaut ? et pourquoi ?
Les formules ne servent à rien si on ne commence pas par comprendre les phénomènes physiques.

Salut,
je reviens sur ce sujet car je suis sur cet exercice, je bloque juste sur la dernière question, si quelqu'un pouvait me guider ça serait sympa 
Et bien c'est justement la ou je bloque, je dirais que
car je pense que V=0
et que W(T)= 0 car le fil est inextensible mais je n'en suis pas sur du tout =/.
Oui, V0 = 0 ("sans vitesse initiale" précise l'énoncé) ; donc (1/2)mV02 = 0
Oui, W(T) = 0 car le fil est inextensible et la force de traction qu'il exerce est à chaque instant perpendiculaire au déplacement ; donc le travail de cette force est nul.
La suite est donc facile...

Donc on en déduit que:
Et que la variation d'énergie cinétique de la bille lorsqu'elle passe de de O en M est donc égal a 0.066 joules.
C'est ça? 


