Inscription / Connexion Nouveau Sujet
Parachutage
Voici un exercice que j'ai dans mon livre chapitre "fonction exponentielle" dans la partie Prépa BAC
Un objet relié à un parachute est largué à l'instant t=0 en un point O.
On admet que sa trajectoire est verticale et que la résistance de l'air est proportionnelle à la vitesse de pénétration dans l'air, on note k le coefficient de proportionnalité. A chaque instant t, exprimé en secondes, on désigne par v(t) la vitesse de l'objet et par h(t) son altitude.
1°) Démontrer que :
m (dv/dt) + kv = mg
où m est la masse totale, en kilos, de l'objet et du parachute et g le coefficient d'accélération de la pesanteur.
Là je suis un peu perdu :/
quand je tourne les page pour voir les exo d'avant je vois que c'est des exo sur les équations différentiel.
Donc je pense que l'exo à un lien avec, mais là je vois pas du tout comment faire ... une petite aide ?
Bilan des forces sur l'ensemble objet + parachute.
1) Poids de l'ensemble (de masse m): P = mg (vertical vers le bas).
2) Force de frottement: f = kv (verticale vers le haut)
3) Poussée d'Archimède dans l'air (elle a été négligée dans cet exercice).
---
Résultante F des forces sur l'ensemble objet + parachute.:
F = |P| - |f| (verticale vers le bas comme sens + pour F)
F = mg - kv
Et a = dv/dt est l'accélération que subit l'ensemble objet + parachute --> F = ma
m.dv/dt = mg - kv
m.dv/dt + kv = mg
-----
Sauf distraction. 
... la suite de l'exercice est comme le début ... tout aussi incompréhensible pour moi ...
2°) on prend :
m = 8 kg
g = 10 m.s-2
et k = 25 USI
On suppose que l'altitude, en mètres, du point O est h(o) = 100 et que la vitesse initial v(o) est nulle
a) déterminer v(t) en fonction de t
Donc je suppose qu'il faut utiliser m.(dv/dt) + kv
0 = m.(dv/dt) + kv
v = - [m.(dv/dt)] / k
?
m.dv/dt + kv = mg
mv' + kv = mg
-----
Solutions de l'équation avec second membre = 0 :
mv' + kv = 0
v = A.e^((-k/m)t)
---
Solution particulière de mv' + kv = mg
v = mg/k
---
Solutions générales de mv' + kv = mg
v(t) = mg/k + A.e^((-k/m)t)
v(0) = 0 -->
0 = mg/k + A
A = -mg/k
v(t) = (mg/k)*[1 - e^((-k/m)t)]
---
Il reste à remplacer m, g et k pat leurs valeurs numériques.
Vérifie quant même la valeur de m, s'il s'agit d'un bonhomme, c'est plus que probablement 80 kg et pas 8 kg
-----
Sauf distraction. 
m.dv/dt + kv = mg
mv' + kv = mg
O_O
le dv/dt qui me gênait tan je pouvais le remplacer par v' ....
Et bien merci beaucoup pour votre aide !!
Pour m c'est bien huit kg, c'est juste un poids attaché à un mini parachute ^^ (et c'est le tout qui fait 8kg)

J'espère que je vais réussir à faire la fin de l'exercice ^^
sinon je repasserai demander encore de l'aide ^^
je me pose une question.
Lorsque un objet tombe ça vitesse est constante ou elle augmente ?
car il me semblais qu'elle était constant xD or la avec v(t) = (mg/k)*[1 - e^((-k/m)t)]
ba elle diminue très très rapidement
elle est d'ailleurs négative :/
Lorsque un objet tombe ça vitesse est constante ou elle augmente
La vitesse commence par augmenter et finit par se stabiliser.
La vitesse est constante à partir du moment où les forces fe frottements équilibrent exactement le poids.

Attention quant-même, quand je dis que la vitesse augmente au début de la chute, c'est évidemment en prenant le sens de la descente comme positif pour la vitesse.

oui mais là j'obtiens une vitesse négative sur:
] 0 ; +inf [
or elle devrait être croissante ou constante me semble t'il :/
Qu'est-ce que tu racontes ?
Où vois-tu que la vitesse est négative ?
m = 8 kg
g = 10 m.s-2
et k = 25 USI
v(t) = (mg/k)*[1 - e^((-k/m)t)]
v(t) = 3,2*(1 - e^(-3,125t))
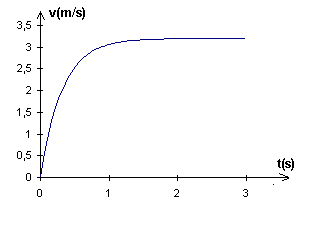
Avec le sens positif de la vitesse vers le bas.

bon ba la suite me bloque aussi -_-"
j'aurais donc eu besoin de l'aide du début à la fin ... super le devoir -_-
pour v(x) j'obtiens:
mv' + kv = mg
mv' = mg - kv
v' = g - (kv)/m
une équation de la forme :
y' = ay + b
avec a = -k/m et b = g
a = -3.2 et b = 10
Donc :
v(t) = Ceat - (b/a)
v(t) = Ce-3.125t + 3.2
or v(o) = 0
donc
0 = C + 3.2
C = -3.2
conclusion
v(t) = -3.2e-3.125t + 3.2
b) En déduire que h(t) = 100 -3.2t - 1.024(e-3.125t-1)
donc je me suis dit comme h(0) = 100
h(t) = h(0) - t fois la vitesse
donc :
h(t) = 100 - t(-3.2e-3.125t + 3.2)
Or ça convient pas à ce que je doit prouver :s
Qu'est-ce que tu racontes ?
Où vois-tu que la vitesse est négative ?
m = 8 kg
g = 10 m.s-2
et k = 25 USI
v(t) = (mg/k)*[1 - e^((-k/m)t)]
v(t) = 3,2*(1 - e^(-3,125t))
je suis désolé
 ... j'ai du mal écrire sur ma calculette
... j'ai du mal écrire sur ma calculette  car j'obtenais pas cette courbe là, et là je l'ai obtenu -_-"
car j'obtenais pas cette courbe là, et là je l'ai obtenu -_-"
pourtant j'ai vérifier plusieurs fois ...
v(t) = -3.2e^(-3.125t) + 3.2
v(t) = h'(t)
h(0) = 100 --> -1,024 + C = 100 , C = 101,024
-----
Sauf distraction. 
ah Oô
on peut dire :
v(t) = h'(t) ?
il me semble que vous utiliser des intégrations :/
or j'ai pas vu ça ... -_-"
je peut pas réaliser l'exercice sans ?
(encore merci de votre aide  )
)
La vitesse est bien la dérivée de l'espace parcouru par rapport au temps.
--> v(t) = h'(t)
Et on a montré que v(t) = 3,2*(1 - e^(-3,125t))
on a donc h'(t) = 3,2*(1 - e^(-3,125t))
C'est une équation différentielle.
La plus simple façon d'en venir à bout est d'intégrer les 2 membres.
Sinon applique ce qu'on a appris mais je ne connais pas les programmes actuels... La seule chose que je sais est qu'ils sont désespérément vides.

s'il vous plait, pourquoi ce signe négatif devant l'intégration ??? je vous en prie, je ne vois vraiment pas... merci d'avance


