Inscription / Connexion Nouveau Sujet
-P.sina+F-f =0 !? Pourquoi ?
Bonjour
Un véhicule, de masse m=1300kg, roule à vitesse constante V=90,0km.h-1 sur une route rectiligne et horizontale. L'ensemble des forces s'opposant à l'avancement est équivalent à une force unique, opposée au vecteur vitesse, de valeur f=800N.
1. Déterminer la valeur de la force motrice développée par le moteur.
2. Le véhicule aborde, à présent, une côte formant un angle de 14,0° avec l'horizontale. Quelle doit être la nouvelle valeur de la force motrice si le conducteur maintient la même vitesse et que l'ensemble des forces s'opposant à l'avancement est toujours équivalent à une force unique, opposée au vecteur vitesse, de valeur f=800N?
1. Pour la question 1 c'est bon.
P+Rn+F+f =0 vectoriellement ( avec P le poids, Rn réaction normale de la route, F la force motrice, F les forces de frottements)
Sur l'axe (O,X) F-f =0 donc F=f
Sur l'axe (O,Y) -p+R donc P=Rn
la er equation donne la solution F=f=800N
2. Principe d'inertie P+Rn+F+f = n
Projection sur (O,X)
-p.sina+F = 0 vectoriellement
-Psina-F=0
et dans le corrigé, la relation est -P.sina+F-f =0 Je ne comprends pas du tout .
Projection sur (O,Y)
Rn+P.cosa =0 vectoriellement
Rn-P.cosa =0 ou -P.cosa+Rn =0
Mais c'est la projection ( O,X) que je ne comprends pas :/
J'espère que vous pourrez m'aider en ces temps de fêtes
Bon réveillon à vous !
-P.cosa
Bonjour,
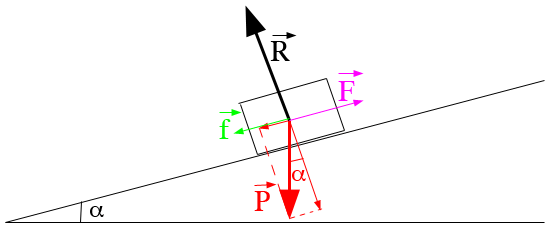
Le schéma ci-joint...
L'axe x est sur le plan incliné, orienté positivement vers le haut.
Donc F est positive, f opposée au mouvement est négative et la projection du poids sur l'axe x (P sin 
) est négatif également.
Donc F - f - P sin = 0 puisque la somme des forces est nulle (vitesse constante).
Sur l'axe y (perpendiculaire au plan incliné et orienté positivement vers le haut), on a R et la projection de P sur l'axe y (P cos ).
R est positive et P cos est négative donc R - P cos = 0
Une voiture dont la valeur du poids est P=8000 N roule à une vitesse constante de valeur v= 90km/h sur une route rectiligne horizontale. L'ensemble des frottements ( air sur la carrosserie et sol sur certains pneus ) est modélisable par une force opposée au mouvement de valeur égale eu 1/10e de celle du poids. la force motrice est de800N
c) Le véhicule aborde maintenant une côte à 10%. Quelle doit être la valeur de la nouvelle force motrice pour que la vitesse reste constante ?
On admet que la pente ne modifie pas les frottements
Note : Une côte à 10% est telle que le véhicule s'élève de 10m pour 100m parcourus.
dans ce cas ( qui est très similaire au problème que j'ai posté ) :
sur l'axe ( O,Y)
Rn-P.cosa=0
Rn =m.g*cosa
Sur l'axe (O,X)
j'ai fait T-P.sina =0
Mais je ne pense pas que ce soit ça finalement 
car ce problème est presque pareil à celui que je viens de poster ..
Donc qu'est-ce que ça devrait etre ? :/
T-P.sina-F=0
J'ai l'impression de faire des problèmes, qui se ressemblent mais qui se contredisent .. :/
Sur l'axe Ox, on a F - P sin - f = 0
F étant la force motrice
Tous ces problèmes de plan incliné se résolvent de la même façon à quelques détails près.
Il faut surtout voir qu'on retrouve l'angle du plan incliné en appliquant le théorème des angles à côtés perpendiculaires (angle rouge sur le schéma).
Annuler
connectez vous