Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Optique lentille convergente

Posté par
labougie 01-10-12 à 12:18

Bonjour,

Sur un banc optique, un objet AB est situé à 12cm devant une lentille convergente de distance focale f'=5.0cm.
Le point A est sur l'axe optique.

1/ Appliquer la relation de conjugaison pour déterminer la position de l'image.
2/ L'objet AB à une hauteur de 3.0cm. Appliquez la relation de grandissement pour déterminer la taille de l'image.
3/ L'image est elle droite ou renversée?
4/ Vérifier ces résultats par une construction géométrique.

-----------------------

1/
Le relation do conjugaison et définie par

\frac{1}{OA'}-\frac{1}{OA}=\frac{1}{f'}

\frac{1}{OA'}-\frac{1}{12cm}=\frac{1}{5cm}

soit \frac{1}{OA'}-\frac{1}{0.12}=\frac{1}{0.05}

Soit \frac{1}{OA'}=\frac{1}{0.12}+\frac{1}{0.05}  soit  \frac{1}{0.17}

2/
La relation de grandissement
L'objet AB à une hauteur de 3.0cm.

\gamma= \frac{A'B'}{AB}=\frac{OA'}{OA}

\gamma= \frac{A'B'}{AB}=\frac{OA'}{OA}

A'B'= AB * \frac{OA'}{OA}

Soit A'B'= 3cm * \frac{17cm}{12cm}

Donc A'B'= \frac{51}{12}Cm soit 4.25 cm

3/
Je suppose que pour qu'une image soit droite, le signe doit être positif, donc pour une image inversée, le signe sera négatif

Le signe étant positif, l'image est alors droite.

4/
Je ne vois pas comment faire le dessin est le poster ici du coup, sauf la faire papier.

Question

Pourquoi a t'on cette notation?  \overline{AB}  ou   \overline{oA'}

Labougie

Posté par
Marc35re : Optique lentille convergente 01-10-12 à 12:36

Bonjour,
Il y a une erreur dans l'application de la relation de conjugaison...
En effet, la relation de conjugaison s'écrit :
\Large \frac{1}{\bar{OA'}}\,-\,\frac{1}{\bar{OA}}\,=\,\frac{1}{f'}
OA et OA' sont en valeurs algébriques !...
Donc, si on oriente l'axe positivement de A vers A', on a :  \bar{OA}\,=\,-\,0,12   ou  -\,12  si on fait les calculs en cm
Il en est de même pour la relation de grandissement :
\Large \gamma\,=\,\frac{\bar{AB'}}{\bar{AB}}\,=\,\frac{\bar{OA'}}{\bar{OA}}
Ce sont des valeurs algébriques.

Posté par
Coll Moderateurre : Optique lentille convergente 01-10-12 à 14:15

Bonjour labougie
Bonjour Marc35

labougie >>
Je te recommande un petit TP ; tu le trouveras sur l'une des pages de "Figures animées pour la physique".
Celle-ci

D'autre part, pour apprendre à insérer une image, une figure, un schéma, un graphique, un tableau (pas un énoncé !) clique sur la maison

Posté par
labougiere : Optique lentille convergente 02-10-12 à 09:51

Bonjour Marc35,
Bonjour Coll,

1/
Le relation de conjugaison et définie par

Citation :
OA et OA' sont en valeurs algébriques
, donc en valeurs absolues ?

\frac{1}{OA'}-\frac{1}{OA}=\frac{1}{f'} \\ \\ \frac{1}{OA'}-\frac{1}{12cm}=\frac{1}{5cm} \\ \\ soit   \frac{1}{OA'}+(-|\frac{1}{0.12}|)=\frac{1}{0.05} \\ \\ Soit   \frac{1}{OA'}=-|\frac{1}{0.12}|+\frac{1}{0.05}  soit  -\frac{1}{0.07}

2/
La relation de grandissement
L'objet AB à une hauteur de 3.0cm.

\gamma= \frac{A'B'}{AB}=\frac{OA'}{OA} \\ \\ \gamma= \frac{A'B'}{AB}=\frac{OA'}{OA} \\ \\ A'B'= AB * \frac{OA'}{OA} \\ \\ Soit   A'B'= 3cm * \frac{7cm}{12cm} \\ \\ Donc   A'B'= \frac{21}{12} cm   soit   1.75 cm

3/
Je suppose que pour qu'une image soit droite, le signe doit être positif, donc pour une image inversée, le signe sera négatif

Le signe étant positif, l'image est alors droite.

4/
Citation :
Je ne vois pas comment faire le dessin est le poster ici du coup, sauf le faire papier.

Merci Coll pour le TP,

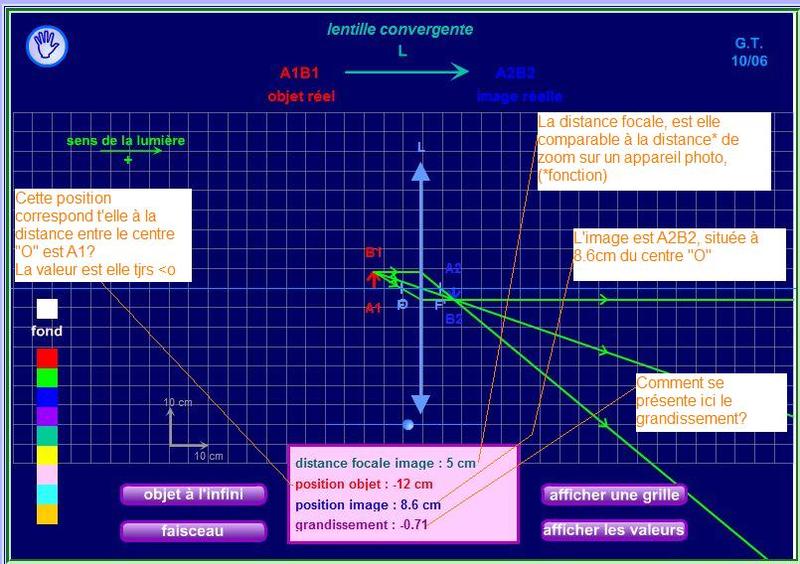
Optique lentille convergente



Pour résumer:
Si mon schéma est bon, alors mon exo ne l'est pas et, bien qu'ayant la correction, mal expliquée dans un manuel,je ne la comprends pô.

labougie

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
Coll Moderateurre : Optique lentille convergente 02-10-12 à 10:31

Toujours commencer par le schéma (je t'ai indiqué comment le poster sur le forum).
Celui-ci est fait avec Geogebra ; mais on peut utiliser un autre logiciel de dessin.

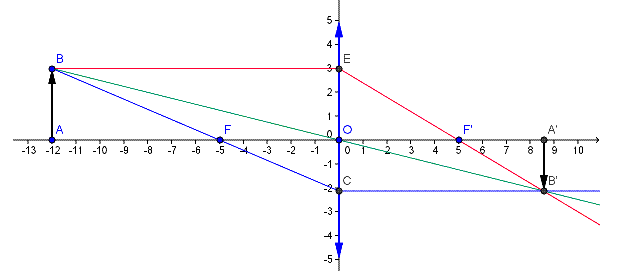
Optique lentille convergente

Les trois rayons dont il faut savoir sans hésiter tracer les trajets :
. le rouge : il est parallèle à l'axe optique et passe donc ensuite par le foyer image F '
. le vert : il passe par le centre optique O et n'est donc pas dévié
. le bleu : il passe par le foyer objet F et ressort donc parallèlement à l'axe optique

Ensuite, c'est de l'optique géométrique
Ce qui signifie qu'il faut considérer des triangles semblables... et l'on trouve ainsi toutes les distances !

Mais ces considérations géométriques sont résumées dans les relations de conjugaisons.
Il ne faut pas utiliser les distances (toujours positives) mais les mesures algébriques des segments.
Ces mesures algébriques sont négatives si le segment est considéré en sens inverse de propagation de la lumière
Ces mesures algébriques sont positives si le segment est considéré dans le sens de propagation de la lumière

Pour l'objet, on considère généralement que le sens de l'objet est positif

En conséquence, ici :

\bar{OA}\,=\,-\,0,12\,\rm{m}
\bar{AB}\,=\,+\,0,03\,\rm{m}
\bar{OF'}\,=\,+\,0,05\,\rm{m}

En appliquant la relation de conjugaison :

\large \frac{1}{\bar{OA'}}\,-\,\frac{1}{-\,0,12}\,=\,\frac{1}{0,05}

On en déduit

\bar{OA'}\,\approx\,+\,0,0857\,\rm{m}

et pour le grandissement

\large \gamma\,=\,\frac{\bar{OA'}}{\bar{OA}}\,=\,\frac{0,0857}{-\,0,12}\,\approx\,-\,0,714
si bien que
\bar{A'B'}\,=\,-\,0,0214\,\rm{m}

L'image est renversée ; sa taille vaut environ 2,14 cm et elle est située après la lentille à environ 8,6 cm

Posté par
labougiere : Optique lentille convergente 02-10-12 à 12:03

J'ai chargé geogebra pour travailler les graphiques.

Je n'arrive pas à reproduire ce calcule

\\ \\ \large \frac{1}{\bar{OA'}}\,-\,\frac{1}{-\,0,12}\,=\,\frac{1}{0,05} \\ \\ On   en   déduit \\ \\ \bar{OA'}\,\approx\,+\,0,0857\,\rm{m} \\

comment procèdes tu pour trouver 0.0857...

Posté par
Coll Moderateurre : Optique lentille convergente 02-10-12 à 12:24

Par exemple :

\large \frac{1}{\bar{OA'}}\,=\,\frac{1}{0,05}\,+\,\frac{1}{-\,0,12}

\large \frac{1}{\bar{OA'}}\,=\,\frac{1}{0,05}\,-\,\frac{1}{0,12}

\large \frac{1}{\bar{OA'}}\,=\,\frac{0,12}{0,05\times 0,12}\,-\,\frac{0,05}{0,12\times 0,05}

\large \frac{1}{\bar{OA'}}\,=\,\frac{0,12\,-\,0,05}{0,05\times 0,12}

\large \frac{1}{\bar{OA'}}\,=\,\frac{0,07}{0,05\times 0,12}

\bar{OA'}\,=\,\frac{0,05\times 0,12}{0,07}\,=\,\frac{0,006}{0,07}\,\approx\,0,085\,714\,\rm{m}

ou \bar{OA'}\,\approx\,8,57\,\rm{cm}

Posté par
labougiere : Optique lentille convergente 03-10-12 à 00:14

Bonsoir Coll,

Arff, mais c'est bien sûre, la mise sous le même dénominateur, je n'étais pas assez concentré, et surtout cela ne met pas venu à l'idée.

1/
Le relation de conjugaison et définie par

\frac{1}{OA'}-\frac{1}{OA}=\frac{1}{f'}

Démontré par Coll,

ou    \bar{OA'}\,\approx\,8,57\,\rm{cm}


2/
La relation de grandissement
L'objet AB à une hauteur de 3.0cm.

\gamma= \frac{A'B'}{AB}=\frac{OA'}{OA} \\ \\ \gamma= \frac{A'B'}{AB}=\frac{OA'}{OA} \\ \\ A'B'= AB * \frac{OA'}{OA} \\ \\ Soit   A'B'= 0.03 * \frac{\frac{0.006}{0.07}}{-0.12}  les nombres sont en cm

Donc   A'B'= -0.0214 m   soit   2.14 cm

3/
Le signe étant négatif, l'image est alors renversée.

Citation :
L'image est renversée ; sa taille vaut environ 2,14 cm et elle est située après la lentille à environ 8,6 cm


4/Capture de Coll

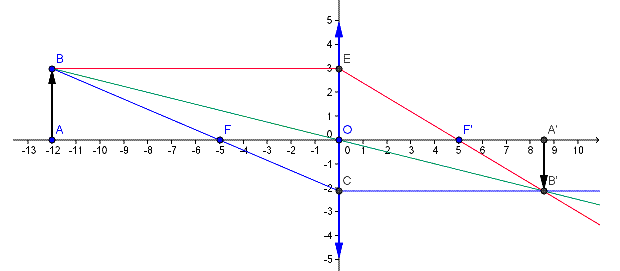
Optique lentille convergente

labougie

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
Coll Moderateurre : Optique lentille convergente 03-10-12 à 07:34

Les notations ont de l'importance.

OA est la longueur du segment qui joint le point O au point A, c'est une distance ; une distance est toujours positive

OA\,=\,12\,\rm{cm}

\bar{OA} est la mesure algébrique du segment qui va de O à A. Traditionnellement on adopte comme sens positif de l'axe celui qui correspond au sens de propagation de la lumière. Sur mon schéma, de la gauche vers la droite. Donc, ici, \bar{OA} est négatif

\bar{OA}\,=\,-\,12\,\rm{cm}

Sans respecter cela il est tout simplement impossible de faire des exercices d'optique géométrique.
______________

Enfin, je te prie de bien vouloir respecter la manière de poster une figure. Les images doivent être placées sur le serveur de l'île :

Posté par
labougiere : Optique lentille convergente 03-10-12 à 08:59

Bonjour Coll,

Merci pour toutes les précisions apportées.

Pour les images à héberger, effectivement j'utilise un hébergeur autre, par habitude sur l'entre-aide que je porte sur un autre forum.
Je travaille en HTML et sur un forum en wysiwyg. (what you see is what you get)
Ma première capture était supérieur à 80ko, pour le scde, j'ai simplement utilisé ton lien, de mémoire.

Je tâcherai de me souvenir de ce détail.
Peut on donner l'url de l'image si elle est hébergée autre que sur l'ile? (par ex imageshack.us)

Labougie

Posté par
Coll Moderateurre : Optique lentille convergente 03-10-12 à 09:14

Attention : ce n'est pas un détail !

Il faut respecter la procédure prévue pour poster les images. Non, les images doivent être hébergées sur le serveur de l'île et il n'est pas autorisé de donner l'url d'un autre serveur.

Si les dimensions ou la taille dépassent les limites autorisées, là encore il est simple de réduire ou de comprimer.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !