Bonsoir,

Et si tu faisais l'effort de recopier mot pour mot et intégralement l'énoncé ?

Bonjour,

Voici l'enonce :

La relation de conjugaison est etablie a partir des proprietes du modèle des lentilles minces. Retrouvons cette relation.

( La suite comporte un schema de lentille convergente)

A- En utilisant le theoreme de Thales, montrer que les rapports OA'/OA et F'A'/F'O sont egaux ( pour cette question, je n'ai pas rencontrer de problème)

B- en appliquant la Relation de Chasles a F'A', retrouver la relation de conjougaison

J'ai commencer en disant que F'O + OA'= F'A' après je bloque

Merci d'avance

Eh bien voilà ! Maintenant on peut comprendre...

"La deuxième question suit toujours la première" (air connu, n'est-ce pas)

Tu as établi que :

        [1]

c'est correct.

Tu as commencé à écrire que :

        [2]

c'est bien ainsi qu'il faut commencer.

Tu connais la relation de conjugaison. Tu sais qu'y figurent , et

Tu en déduis facilement laquelle des trois mesures de l'équation [2] il faut remplacer par sa valeur issue de l'équation [1]

Attention : utilise les mesures algébriques (et pas les simples longueurs des segments)

Bonjour,

Alors voilà ce que je trouve:

OA'/OA = F'O/F'O+ OA'/F'O
       = 1+OA'/F'O


( Le tout etant des valeur algebriques )


Merci

Ce n'est pas fini.

Il te reste à diviser chaque membre par
et par faire apparaître la distance focale

Je ne suis pas sure du tout de ce que j'avance ;

1+OA'/ F'O

= -1/OA' - F'O/ OA'

( Toujours en mesure algebrique )

Par contre je ne vois pas comment calculer la focale

Merci

Je ne comprends pas très bien.

Tu étais arrivée (message de 18 h 18) à :



Tu divises chaque membre par :



Tu arranges un peu cela :



et la dernière étape...

À toi !

Alors est ce que c'est :
-1/OA'-1/0A= 1/OF'
??


Merci de votre aide

Je considère que le premier signe "moins" est une faute de frappe...

Puisque

on déduit immédiatement :



Qui est la forme "habituelle" de la relation de conjugaison.

D'accord, merci de votre aide

Je t'en prie.
À une prochaine fois !

Excuser moi,
Mais je n'arrive pas à la première partie de cet exercice(A) est ce que vous pourriez m'aider svp

Bonjour,

Il faut faire un schéma.
Utiliser les trois rayons classiques appris en cours
Appliquer le théorème de Thalès appris en quatrième au collège.

daccord merci

Je t'en prie.
À une prochaine fois !

Pouvez vous svp m'aider a répondre à la première question car je suis bloquée

Le théorème de Thalès :
Si deux droites parallèles (cB)//(MN)

AB/AM= AC/AN=BC/MN
Non ?
Pour notre exemple nous avons besoin de comparer les triangles BOD et DOF'
Et F'A'B' non ?
Mais je n'ai aucune idée à part cela
Merci pour votre aide 😃

Hé bien du coup,

si tu fais le schéma optique de cet exercice, tu n'as pas l'impression de retrouver une configuration de Thalès vue en troisième ?

Du coup, tu en déduis une égalité du même genre non ?

Du coup ma configuration de Thalès est :
DO//A'B'
Donc cela me donne :
DF'/F'B'= DO/A'B'=A'F'/F'O
Mais dans le triangle BDO je suppose que BD=AO
J'avance ?? :/

Qu'est-ce que le point D ?
Tu n'expliques pas tes notations.

Je te propose d'utiliser le schéma qui suit :

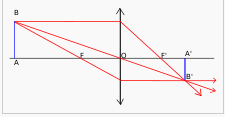
J'appelle D le point d'intersection du rayon provenant de B étant parallèle a l'axe optique et de la lentille  ( j'ai fait exactement le même schéma )
Avec votre configuration je propose :
A'B'//AB
Ce qui me donne :
A'B'/AB=A'O/OA=BO/OB'
Mais je n'arrive pas a conclure juste avec cela que F'A'/F'O
Merciiii pour votre aide

Si on regarde donc avec ces notations :



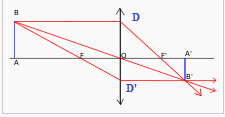
Les triangles OAB et OA'B' sont semblables donc d'après le théorème de Thalès :

A'B'/AB = OA'/OA

Et d'après notre schéma, on a également :

AB = OD

A'B' = OD'

Or les triangles F'OD et F'A'B' sont également semblables donc d'après le th. de Thalès :

A'B'/OD = F'A'/F'O

et comme on a vu que OD = AB on a

A'B'/AB = F'A'/F'O

Compris ?

Ouiiiiiiiiiiiiiiiiii , j'ai compris merci énormément pour votre aide 😊

de rien

A+

Bonjour,
excusez moi,
j'ai le même exercice et je ne vois pas commencer utiliser le théorème pour montrer que les rapports sont égaux..

Bonjour,

Cf. la schématisation du pb.

Ce n'est qu'une simple application du th de Thalès vu en 3ème.

Oui mais avec quels triangles ?

Mais je l'ai déjà expliqué dans un message antérieur :

Citation :
Si on regarde donc avec ces notations :



Les triangles OAB et OA'B' sont semblables donc d'après le théorème de Thalès :

A'B'/AB = OA'/OA

Et d'après notre schéma, on a également :

AB = OD

A'B' = OD'

Or les triangles F'OD et F'A'B' sont également semblables donc d'après le th. de Thalès :

A'B'/OD = F'A'/F'O

et comme on a vu que OD = AB on a

A'B'/AB = F'A'/F'O

Compris ?

Oui mais nous ce qu'on veut c'est OA'/OA = F'A'/F'O

Ah non c'est bon j'ai compris! Merci

Ouf !

De rien, A+