Bonsoir jesstev,

ton dm est pour demain dis-tu ? et tu t'inquietes seulement maintenant ("Posté le 27-09-11 à 20:28") ? Et, autre remarque genante : "L'image ci-dessous ", mais il n'y a pas d'image ci-dessous (ci-dessus non plus d'ailleurs).

Alors je te propose un marche : tu mets sur le forum toutes les indications necessaires pour trouver la solution de ton exercice, et demain je te poste la solution (mais il sera sans doute trop tard pour ton dm,), ou tu laisses tomber et la prochaine fois que tu dois poster sur ce forum tu essaies de faire ca dans les regles. Tu recevras alors une aide efficace dont tu pourras vraiment tirer profit.

Bonne fin de soiree, Prbebo.

Bonsoirs, eu oui en effet il est trop tard je pense, j'ai essayé de le faire on verra.
La prochaine fois j'essayerais de m'y prendre en avance et de bien mettre l'énoncé.

Enfin merci quand même.

Bonjour jesstev,

mon message d'hier soir était sans doute un peu sec, mais... c'est aussi pour ton bien ! Il y a sur ce forum plein de gens disponibles et compétents qui ne demandent qu'à t'aider, mais encore faut-il leur en laisser le temps.

Mon marche proposé ci-dessus tient toujours, et pour  te prouver que ce n'est pas un marché de filou voici les réponses a ton exercice :

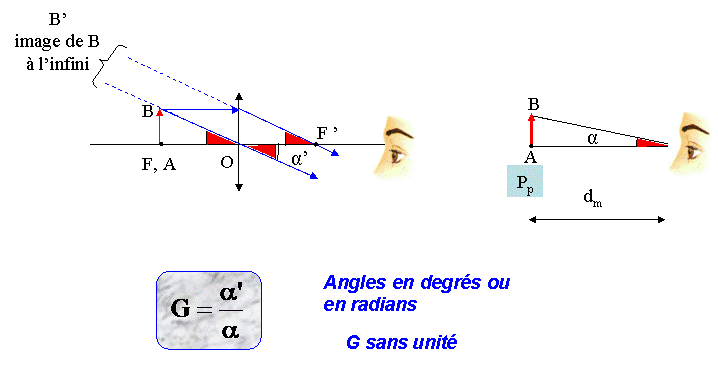
a) l'image donnée par une loupe est toujours à gauche de celle-ci, plus exactement du meme coté que l'objet. Elle peut ainsi etre éloignée de l'oeil pour que celui-ci puisse la voir "a l'infini", cad sans fatigue. C'est sans doute ce qu'a montré l'image non jointe a l'énoncé.
Puisque l'objet est réel et que l'image est restée du meme coté que l'objet, cette image est virtuelle. Elle est donc de meme sens que l'objet et agrandie.

b) La loupe a une distance focale OF' = f' = 1/P ou P est la puissance en dioptries. On obtient donc f' = 1/20 soit 0.05 m (5 cm).
Pour que l'objet A possède une image virtuelle donnée par la loupe, il faut que A soit placé entre le foyer objet F et le centre optique O de cette loupe. Comme la distance FO vaut aussi 5 cm (= f'), il faut que AO 5 cm.

c) Conséquence directe de la réponse a b) : si A est placé en F (maximum de la distance demandée en b), son image est a l'infini. Il faut donc que AO = 5 cm.

d)  voir schéma ci-dessous : on montre facilement que l'angle ' (figure 1) est tel que tan' = AB/FO, soit aussi AB/f'. Avec AB = 3 mm et f' = 5 cm, on obtient ' = 3.43 degrés.
Voir figure 2 : tan = AB/d_m, ou d_m est la distance minimale de vision distincte (25 cm ici). On obtient = 0.688 degrés.
On obtient alors '/ = 5 aux arrondis près.

Quelques remarques :

a) le point le plus proche de l'oeil ou l'objet peut etre placé pour etre vu net (en accommodation maximum) s'appelle "punctum proximum" (Pp sur la figure 2). Par opposition au punctum remotum, qui est le point le plus éloigné pouvant etre vu nettement (l'infini pour un oeil sans défaut).

b) Les angles et ' étant petits, on peut se dispenser de calculer leur tangente. En effet on montre en maths que pour un angle petit, tan est pratiquement égal a exprimé en radian. Tu peux vérifier facilement que ' = 3.43 degres = 0.06 radians, et que cette valeur est aussi celle de sa tangente.

c) La quantité G = '/ s'appelle "grossissement". Il n'a pas d'unité.
On n'est pas obligé de calculer et pour connaitre G. Un raisonnement simple montre que G = P.dm, P puissance de la loupe en dioptries, dm distance minimale de vision distincte en mètres (0.25 m ici).


Voilà. Au plaisir de te retrouver bientot sur ce forum.

Prbebo

Bonjour
Désolée de remonter le message mais j'ai eu le même exercice à faire mais je ne comprends pas comment on place l'angle alpha sous lequel est vu l'objet lorsqu'on le regarde directement en se placant à 25 cm. Et quand on dit "25 cm" c'est à 25 cm de la lentille?
Merci d'avance pour votre réponse

Merci beaucoup prbebo tu m'as vraiment bien éclairé.

Bonjour jessstev,

a ton service pour une prochane fois.  B.B.

Bonjour,
Je fais moi aussi le même exercice et je ne comprends pas trop la question c) surtout que dans mon livre on me demande en plus de faire un schéma. Pourriez-vous m'expliquer un peu plus en détail cette question là ?

Merci

Bonsoir Mademoisel,

desole pour l'attente, mais je suis occupe sur le forum superieur avec plusieurs topics... Pour la question c, aucune difficulte : on desire obtenir de l'objet AB une image A'B' situee a l'infini : a ton avis, dans quel cas de figure une lentille mince donne d'un objet A une image A' a l'infini " La reponse est dans dans ton cours : c'est lorsque A est confondu avec le foyer objet F de la lentille. Et si on a un objet AB de dimension donnee, il faut que cet objet soit dans le plan focal objet de la lentille (c'est le plan perpendiculaire en F a l'axe optique). Inutile de refaire un schema : regarde le premier que j'ai fait dans ma reponse du 28/09, c'est exactement ca.

Si tu as encore des pb de comprehension n'hesite pas a m'ecrire... mais demain, pas ce soir car je ne vais pas tarder a couper le contact !

Prbebo.

Bonjour,

Ah d'accord je vois, maintenant c'est plus clair.

Merci Beaucoup pour votre aide.

Bonjour à tous!
Moi aussi j'ai un exercice de ce type que je ne comprends pas très bien, est-ce que ça vous dérangerai de me l'éclaircir un petit peu, s'il vous plaît. Je ne sais pas si mon schéma est exact du coup, je bloque pour les questions suivantes.. Merci d'avance.
https://www.ilephysique.net/sujet-optique-250291.html

D'ailleurs, pour la tangente a', je trouve 2.86 degrés comment trouvez-vous 3.43 degrés?

Salut moi aussi c'est la même énoncé mais la c) c'est on examine un objet de ABde 3.0mm avec cette loupe de façon à obtenir une image à l'infini .Quelle est alors la distance entre l'objet et la lentille ? Réaliser un schéma