Inscription / Connexion Nouveau Sujet
Ondes mécaniques
Bonjour, voici un exercice que j'ai à faire pour mon prochain cours le problème est que je bloque à un moment, pouvez-vous m'aider?🤗
Énoncé - Question - Documents - Début de réponse
.
.
.
Un tsunami est une onde produite par le brusque déplacement d'un volume très important d'eau, résultant en général, d'un séisme. Le brusque mouvement d'eau donne naissance à une série d'ondes, de très grandes longueurs d'onde, de l'ordre de la centaine de kilomètres.
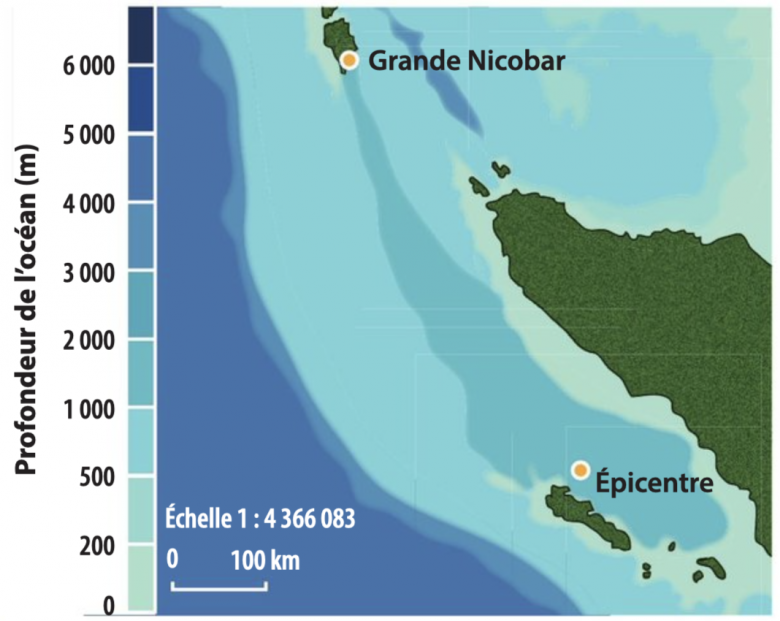
Le 26 décembre 2004, à la suite d'un tremblement de terre dans le centre de l'Indonésie, une vague s'est abattue sur l'île de Grande Nicobar. Le foyer du séisme a été localisé à 30 km de profondeur, au sud de Grande Nicobar. L'épicentre est représenté sur la carte ci-dessous.
De combien de temps les habitants de l'île de Grande Nicobar auraient-ils disposé pour se mettre à l'abri s'ils avaient été prévenus dès l'instant où le séisme s'est produit ?
Doc + : On peut classer les ondes de surface, suivant leurs caractéristiques et celles du milieu de propagation. Deux types d'ondes sont présentés ci-dessous :
- Ondes courtes : lorsque la longueur d'onde 
est faible par rapport à la profondeur locale h de l'océan (au moins , 0,5 h). Leur célérité v est donnée par :
- Ondes longues : lorsque la longueur d'onde est très grande par rapport à la profondeur h de l'océan ( . 10 h), les ondes sont appelées des ondes longues. Leur célérité v est définie par :
Avec g = 9,8 m.s-2
Échelle su schéma : 1 cm <-> 100 km soit 470 km (4,7cm) sépare l'épicentre du séisme de Grande Nicobar. On voit que sur les 240 premiers km (2,4cm), la profondeur de l'océan est de 1 000 m alors que sur les 230 derniers km (2,3cm) la profondeur de l'océan est de 500m.
.
.
.
Merci d'avance🤗
Bonjour,
On peut classer les ondes de surface...
un tsunami n'est pas une onde de surface.
Au large, la vitesse de propagation du tsunami est :
V =
(gh)
h étant la profondeur.
Elle ne dépend pas de
Oui en effet c'est une erreur en recopiant l'énoncé.
Donc si j'ai bien compris je n'utilise jamais la première formule ?
Mais toujours celle-là ?
Oui, car le tsunami est une "onde longue" (en reprenant la terminologie du doc.) puisque sa longueur d'onde (
100 km) est très supérieure à la profondeur (≤ 1km)
On est en eau dite "peu profonde" ( pour un tsunami)
En revanche, pour la houle , il faudrait appliquer l'autre formule , car sa longueur d'onde est bien plus petite!
Et je ne comprend pas comment savez-vous que la longueur d'onde tsunami est de 100km et la profondeur 1km. Alors quand dans l'énoncé on nous dit que sa profondeur est de 30 km et que j'ai calculer un longueur de 470 km
C'était juste un exemple? où je n'ai pas compris...
Beaucoup de confusions !
Le brusque mouvement d'eau donne naissance à une série d'ondes, de très grandes longueurs d'onde, de l'ordre de la centaine de kilomètres.
Ça me paraît clair.
On voit que sur les 240 premiers km (2,4cm), la profondeur de l'océan est de 1 000 m
C'est toi même qui l'as écrit!
En effet de grosse confusion j'ai compris cette partie là donc :
on cherche le temps que met l'onde à se propager soit t = d/v et
On voit que sur les 240 premiers km (2,4cm), la profondeur de l'océan est de 1000
m
Soit avec t en s; d = 240x103m; h = 1 000m et g = 9,8 m.s-2 :
.
.
Pour l'instant es-ce correcte?
puisse garder 2424? on aura un résultat avec h, min et s comme ça.
On voit que sur les 230 derniers km (2,3cm) la profondeur de l'océan est de 500m
Soit avec t en s; d = 230x103m; h = 500m et g = 9,8 m.s-2 :
Soit t1 + t2 = 2424 + 3286 = 5710 s
5710 s est environ égal à 1H 35min et 17s
Les habitant aurait disposé de 1H 35min et 17s pour se mettre à l'abri.
.
.
Es-ce correcte?
Oui, effectivement, pour un résultat intermediaire comme t1 il faut garder tous les chiffres.
Donc on trouve finalement 1h35
Mais c'est faux car tu as pris la profondeur la plus faible pour chaque couleur, donc tu as minimisé la vitesse du tsunami, qui va donc arriver avant!
Il faut prendre la valeur haute pour chaque couleur pour obtenir un delai sûr
D'accord donc :
Soit t1 + t2 = 1714 + 2323 = 4037 s
4037 s est environ égal à 1H 07min et 28s
Les habitant aurait disposé de 1H 07min et 28s pour se mettre à l'abri.
.
.
Es-ce correct maintenant?
D'accord, je vous remercie krinn de m'avoir aidée dans cet exercice si tout est bon je vous souhaite une bonne soirée🤗
Annuler
connectez vous