Bonjour tout le monde,
vous pouvez me dire comment je dois procéder pour résoudre la 2. a) cette exercice. Je suis un peu perdu
Merci d'avance pour votre aide.

Voici l'énoncé :

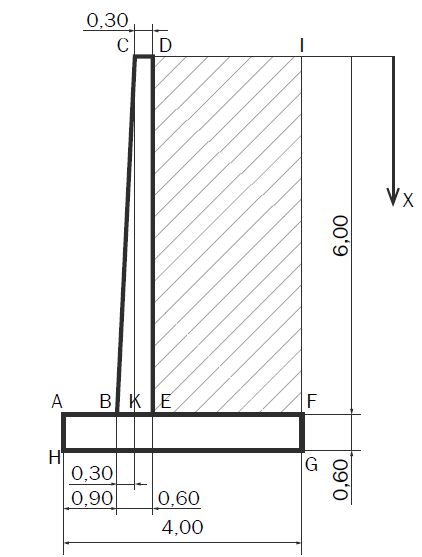
On considère un mur de soutènement ayant la forme et les dimensions représentées sur le schéma page sui-vante.
Il s'agit d'un mur en béton armé que l'on suppose bien dimensionné pour résister aux efforts auxquels il est soumis.
On se bornera, dans cet exercice, à vérifier sa stabilité
générale, tant au renversement qu'au glissement.

Les questions :

2.a) Le mur est soumis, outre son poids propre, à la pous-sée des terres. Cette poussée peut être assimilée à une poussée hydrostatique d'intensité p(x) = 0,6 x N / cm2 où x est exprimé en mètres.
• Quelle est la pression des terres au droit du point G de l'ouvrage (face inférieure de la semelle) ?
• Quelle est la valeur de la poussée totale des terres sur une tranche de mur de 1,00 m de largeur ? Où s'applique-t-elle ?

2.b) En supposant que le mur puisse pivoter autour de son arête H, calculez le moment des forces de renverse-ment et le moment des forces de stabilisation pour une tranche de mur de 1,00 m de largeur.
On prendra pour poids volumique de la terre en place : 18 000 N/m3 ; et pour poids volumique du béton armé : 25 000 N/m3.

Calculez le rapport : Moment de stabilisation / Moment de renversement .
Vous paraît-il suffisant pour assurer la stabilité du mur avec un coefficient de sécurité de 1,5 ?

2.c) En supposant que l'ensemble puisse glisser sur un
plan horizontal HG, vérifier la stabilité au glissement, en prenant comme coefficient de glissement béton/sol
égal à 0,6.
Ici aussi, on prendra un coefficient de sécurité de 1,5.