Dans un référentiel terrestre (qu'on peut considérer comme galiléen pour ce problème).

Juste avant d'être lachée, la balle avait la même vitesse horizontale que le cycliste, sot par exemple V1 cette vitesse.

Lorsque la balle est lachée, la seule force qui s'exerce sur elle est son poids (qui est vertical vers le bas).
Il n'y a donc aucune force (en négligeant les effets du frottement de l'air sur la balle) sur la balle dans une direction horizontale...
Et donc la composante horizontale de la vitesse de la balle reste constante pendant la chute de la balle (soit V1 cette vitesse horizontale).
Le déplacement de la balle dans le sens horizontal est donc x(t) = V1.t

Réfléchissons maintenant sur la composante verticale de vitesse de la balle.
Comme elle est soumise à son poids, la balle subit en vertical l'accélération de la pesanteur (g).
En notant Vy la composante verticale de vitesse de la balle et y(t) la distance qu'elle parcourt en vertical, on a :
Vy(t) = -gt
y(t) = yo - gt²/2

yo est la hauteur de la balle par rapport au sol au moment où elle est lachée.

Les équations paramétriques de la trajectoire de la balle en fonction du temps sont donc :

x(t) = V1.t
y(t) = yo - gt²/2

Pour trouver la trajectoire de la balle (donc l'équation de la courbe qu'elle décrit dans l'espace), il suffit d'éliminer t entre les équations ci-dessus.

x = V1.t
y = yo - gt²/2

t = x/V1

y = yo - g.(x/V1)²/2
y = yo - (g/(2V1²)).x² (c'est l'équation de la trajectoire de la balle ... qui n'est pas une droite, mais bien un arc de parabole.

Exemple numérique :
Supposons la vitesse du vélo : V1 = 5 m/s, la hauteur d'où la balle est lachée = 1 m, avec g = 10 m/s² (pour simplifier les calculs), on aurait:

y = 1 - (10/(2*5²).x²
y = 1 - 0,2.x²

Voila donc ce que verrait, comme trajectoire de balle, un observateur fixe par rapport à la Terre.



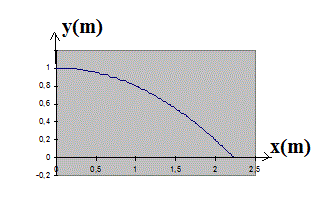
C'est un arc de parabole ... pas une droite.

Je ne comprends toujours pas