Inscription / Connexion Nouveau Sujet
mouvement circulaire et uniforme
Bonjour,
On considère l'enregistrement qui donne les positions successives d'un mobile autoporteur à différentes dates: t1,t2,etc. espacées d'une même durée t=20ms.
1-1 Quelle est la nature du mouvement? Calculer la vitesse angulaire et la vitesse linéaire du point A.
Calcul de la vitesse angulaire:
Voici ce que j'ai trouvé:
Le mouvement est visiblement circulaire et uniforme , les points A1, A2, ... sont équidistants.
On mesure l'angle A1A3  40°, valeur que l'on doit exprimer en radians.
40°, valeur que l'on doit exprimer en radians.
40* /180 = 2
/180 = 2 /9 = 0,70 rad.
/9 = 0,70 rad.
La vitesse angulaire , est par définition, donnée par  =
=  /
/ t avec
t avec  = 0,70 rad. et
= 0,70 rad. et  t = 2*t
t = 2*t
Ce qui donne  t = 2*20 = 40 ms = 0,04s
t = 2*20 = 40 ms = 0,04s
 = 0,70/0,04 = 17,5rad/s
= 0,70/0,04 = 17,5rad/s
La vitesse angulaire est de 17,5rad/s.
Est-ce juste?
Mamie

Calcul de la vitesse linéaire:
On utilise la relation liant la vitesse linéaire à la vitesse angulaire: v= *R
*R
Il faut mesurer le rayon de la trajectoire soit ici 4cm = 0,040m
On trouve donc: v= 17,5*0,040=0,7m/s
Il vaut mieux mesurer sur un plus grand angle ... cela diminue les imprécisions.
---------------
Sur mon écran, le soit-disant cercle ressemble à une patate.
En repérant la croix du dessin par un point O

Si je mesure par exemple les segment de droite [OA1] et [OA9] ne sont pas égaux (et pas rien qu'un peu)
Donc, soit le mouvement n'est pas vraiment circulaire, soit le dessin est bien mal dessiné ... mais alors, mesurer des angles sur un tel dessin et s'en servir pour calculer n'est pas très sain.
Si on place le A16 et A 17 avec l'angle (A15 O A16) = angle (A15 O A16) = angle (A16 O A17), on mesure sur le dessin ; angle (A17 O A1) = 12,5 °
Donc le drand angle (A1 O A17) mesure 360 - 12,5 = 347,5°
Et il est parcouru sur un intervalle de temps Delta t = 16 * 20 = 320 ms
---> un tour complet est parcouru en 320 * 360/347,5 = 331,5 ms
w = 2Pi/0,3315 = 19 rad/s
---------
Avec une imprécision grande à cause du dessin foireux ... et si le mouvement est bien circulaire.
Remarque que la valeur numérique (pour la vitesse angulaire) de ma réponse est peut-être plus éloignée que la tienne de ce qu'attend ton prof.
On ne peut pas vraiment faire quelque chose de correct à partir de la patate donnée comme dessin.
Ma méthode, diminue l'imprécision sur la lecture de l'angle et donc est meilleure que la tienne à ce point de vue.

Bonsoir JP et merci,
DE mon côté j'ai essayé aussi en mesurant l'angle A1A6 et trouvé 19,20 rad/s qui correspond à peu près à ce que tu as écrit, mais quand on passe à la résolution de la vitesse linéaire:
je mesure le rayon = 4cm sur A1 ou 3,5 cm sur A6
Si je prends 4 cm = 0,04m , je trouve v= 19,20*0,04 = 0,77m/s
Si je prends 3,5 cm = 0,035, je trouve 0,672 m/s
pour la première solution , la vérif ne tombe pas juste: V2(A) = A1A3 =environ A1A3 = 2,8 cm = 0,028
V2(A) = A1A3/2*20 = environ 0,028/40 = 0,0007 ce qui ne correspond pas.
Je ne sais pas quoi faire.
Tu fais 2 erreurs :
1) les delta T entre 2 points sont 20 ms et tu as écrit ton calcul comme si c'était 2 s.
V2(A) = A1A3/(2*20.10^-3) = 0,028/(40.10^-3) = 0,7 m/s (c'est déjà moins faux).
2)
Et ceci est trop petit comme valeur, car la distance parcourue n'est pas le segment de droite [A1A3] mais bien la trajectoire curviligne A1A3 qui est plus grande... et donc v > 0,7 m/s calculé ci-dessus

Je me suis dit et si je refaisais le cercle en partant du centre et mettant chaque point A sur le cercle.
J'ai donc trouvé:
Je mesure donc l'angle A1A3 = 45° valeur que l'on doit exprimer en radians.
45*pi/180 = pi/4 = 0,785 rad.
La vitesse angulaire , est par définition, donnée par  =
= /
/ tavec
tavec = 0,785 rad et
= 0,785 rad et  t=2*t.
t=2*t.
Ce qui donne  t = 2*20 = 40 ms = 0,04s
t = 2*20 = 40 ms = 0,04s
= 0,785/0,04 = 19,5 rad/s
La vitesse angulaire est de 19,5rad/s.
Pour la vitesse linéaire, j'ai d'après mon dessin rectifié: R= 3,6 cm = 0,036m
V= 19,5* 0,036 = 0,70
V2(A) = "arc "A1A3 =environ "corde" A1A3 = 2,8 cm = 0,028
V2(A) = "corde"A1A3/2*20 = environ 0,028/40 = 0,0007
Qu'en pense-tu?
V2(A) = "corde"A1A3/2*20 = environ 0,028/40 = 0,0007
oups!!! V2(A) = "corde"A1A3/2*0,02= environ 0,028/0,04 = 0,70m/s

J'ai posé la question à mon prof tuteur pour savoir si c'est normal que le cercle ne soit pas droit, voici ce qu'il m'a répondu/
REPONSE Bonjour, Les points symbolisés par un petit carré noir sont bien sur un cercle dont le centre est désigné par une croix. Peut-être que votre livret de devoirs a été mal imprimé.
En "détordant" l'image, j'obtiens ceci :

Angle de 307,5° parcouru en 14 * 20 = 280 ms
w = (307,5 * Pi/180)/0,28 = 19,2 rad/s
Et un point de la périphérie (avec R = 4 cm) a une vitesse :
v = w*R
v = 19,2 * 0,04 = 0,77 m/s

Pour la suite de l'exercice:
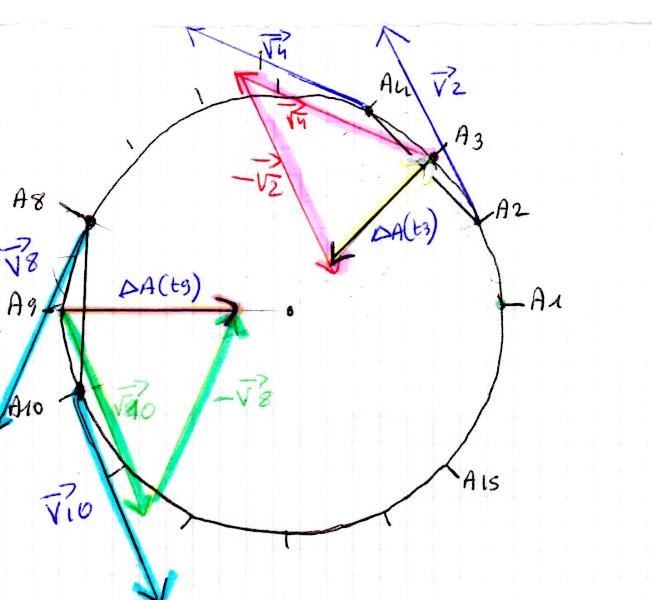
11-2 Tracer les vecteurs variation de vitesse aux dates t3 et t9.
On rappelle que: A(t3) =
A(t3) = A (t4) -
A (t4) -  A(t2)
A(t2)
 A(t9) =
A(t9) = A (t10) -
A (t10) -  A(t8)
A(t8)
Quel est le point de concours des droites d'actions de ces vecteurs.
Pour cette question je ne comprends pas tout merci de votre aide.
Voici le schéma:
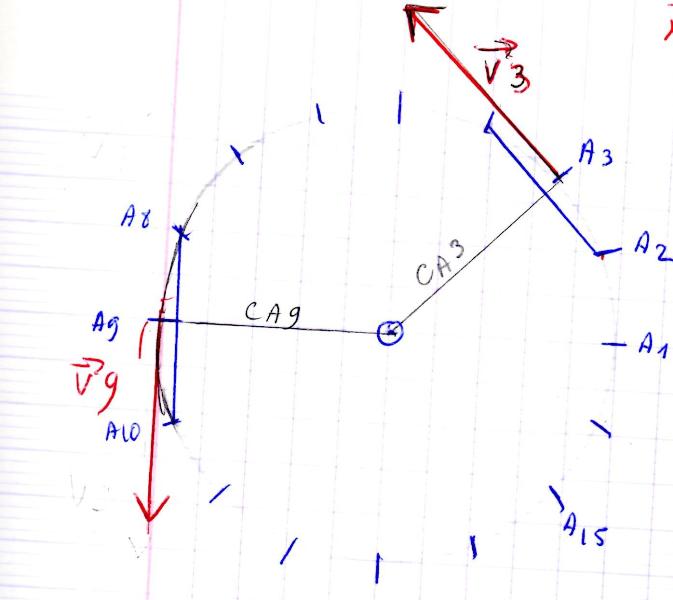
Voila pour la variation de vitesse à la date t3

On voit que le vecteur variation de vitesse pointe vers le centre du cercle.