Inscription / Connexion Nouveau Sujet
Mouvement 1ère
Bonjour,
J'ai des difficultés à retrouver la bonne réponse.
Voici l'énoncé :
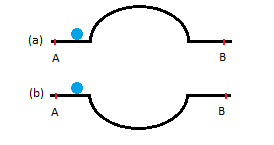
Une bille de masse m est lancée avec une vitesse initiale v0 sur une piste. La forme de la piste peut adopter deux configurations, représentées sur les schémas (a) ou (b). On s'intéresse au temps de parcours entre le point A et le point B (on néglige les frottements).
Montrer que la bille met plus de temps à parcourir
la distance [AB] sur le chemin (b) que
sur le chemin (a).
Intuitivement la bille devrait mettre le même temps à parcours les deux chemins puisque les phases de montée et de descente devraient se compenser... Maintenant, que dit la physique ?
Hello
Montrer que la bille met plus de temps à parcourir
la distance [AB] sur le chemin (b) que
sur le chemin (a).
En es tu certain(e)?
Ce qui est certain c'est que dans les 2 cas la bille arrive en B avec la vitesse v0 (conservation de l'énergie mécanique)
Pour "sentir" pourquoi une des billes va arriver avant l'autre (celle passant par (b)
 )
)
Je te propose de "simplifier" les parcours comme le schéma ci dessous. Ils ont mérite de pouvoir calculer facilement par la résolution d'équations du 2nd degré. La raison de la différence des temps de parcours y apparait cependant
Un autre façon de le sentir est d'imaginer que tu que tu fais ces parcours à vélo (sans assistance électrique
 )
)
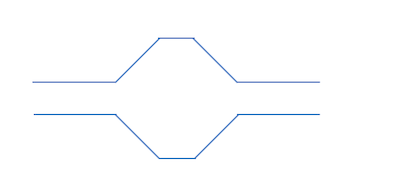
Oh, merci beaucoup, je visualise bien mien !
C'est simplement que Δz n'est pas constant en fonction du temps.
Si on dérive la position on a une droite croissante dans la descente et l'inverse dans le montée, ce qui explique que la vitesse dans la descente a un poids plus important dans la vitesse globale...
Erreur, la vitesse dans le milieu du parcours et non pas dans la descente.
Ce qui explique votre simplification.
Hum je suis content que tu visualises bien mieux, parce que moi ... je n'ai pas trop compris ce que tu as écrit 
Pour le dire avec des mots:
D'un côté on a un parcours où:
- d'abord on monte de A en S (le sommet)
- puis on descend de S en B
De l'autre on a un parcours où:
- on descend de A en F (le fond)
- puis on remonte de F en B
Sur les premières phase des parcours (A en S et A en F)
Il est clair que la bille arrive plus tard en S (elle monte, la pesanteur la ralentit) qu'elle n'arrive en F (elle descend la pesanteur la "pousse")
Dans les 2eme phases (descendante pour la première, montante pour la seconde), la bille passée par S n'a aucune chance de refaire son retard car elle va descendre moins vite que ne descendait la bille passée par F sur la portion descendante de son parcours: pour la simple raison que sa vitesse en début descente est inférieure à v0 (la montée l'a ralentie)
Dans les 2eme phases (descendante pour la première, montante pour la seconde), la bille passée par S n'a aucune chance de refaire son retard car elle va descendre moins vite que ne descendait la bille passée par F sur la portion descendante de son parcours: pour la simple raison que sa vitesse en début descente est inférieure à v0 (la montée l'a ralentie)
Mais dans cette explication vous ne montrez pas que l'accélération positive due à la montée de la balle en F ne va pas compenser l'accélération négative due à la descente de la balle en S ?

Ce que je voulais dire c'est que si vous prenez la dérivée seconde de la position en y vous obtenez bien deux morceaux de droite qui amènent à pondérer la vitesse dans la partie centrale, me semble-t-il ?
Ce que je veux dire, c'est que votre explication ne s'appliquerait pas dans le cas d'une piste formant des segments ?
Mais dans cette explication vous ne montrez pas que l'accélération positive due à la montée de la balle en F ne va pas compenser l'accélération négative due à la descente de la balle en S ?
Dans la montée l'accélération est "négative"
en se sens que dans l'expression
Je t'ai proposer initialement des profils de parcours à pentes constantes pour simplifier le raisonnement et considérer le terme a comme constant (ce qui permet d'écrire les 2 équations ci dessus)
c'est que votre explication ne s'appliquerait pas dans le cas d'une piste formant des segments
Bien sûr que si, je ne connais pas ton niveau en maths ou en informatique mais je t'engagerais à prendre les profils de parcours simplifiés que j'ai dessiné ce matin (disons chaque segment fait 1 m, la vitesse initiale est 10 m/s et la pente 45 °)
tu peut poser les équations du 2nd degré s(t) et pour chaque segment calculer t tel que s(t) = 1 m tu trouveras bien que le parcours "du haut" prend plus de temps et que cela provient des vitesses initiales en début de chaque portion