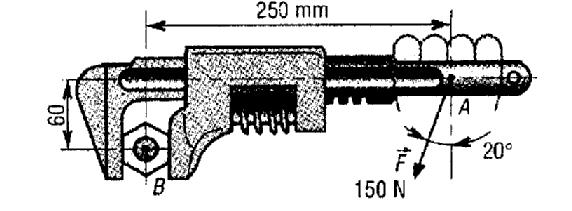
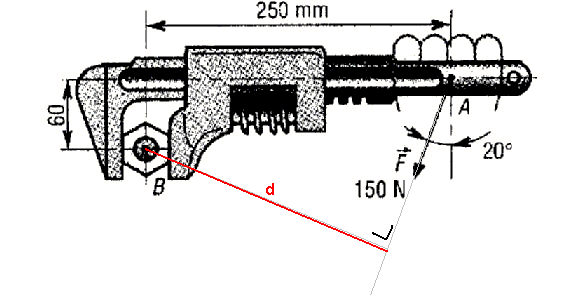
d = 214,4 mm = 0,2144 m (calcule-le)

Couple de serrage = F * d = 150 * 0,2144 = 32,2 Nm

Vérifie

M(F;B) = - 0,250.F.cos(20°) + 0,060.F.sin(20°)
= - 37,5.cos(20°) + 9.sin(20°)
= - 29 ,082 mN

Reprends ta calculette et refais le calcul :
- 37,5.cos(20°) + 9.sin(20°) pour voir.

-32,2 mN

MErci ....

Une méthode parmi d'autres :



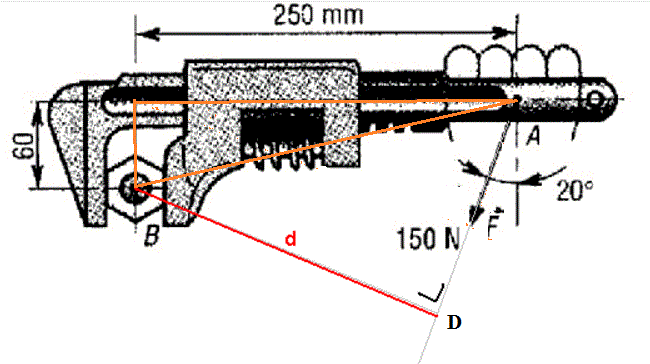
Dans le triangle en orange sur le dessin :

AB² = 250² + 60² = 66100

Soit alpha l'angle en A dans le triangle orange : 60 = 250 * tan(alpha) --> alpha = 13,496°

Soit beta l'angle (BAD) : beta = 90° - 20° - 13,496° = 56,504°

Dans le triangle ABD : BD = AB.sin(beta)

BD = RCarrée(66100) * sin(56,504°)

BD = 214,4 mm

Sauf distraction.  

Merci beaucoup, c'était très clair !

Bonsoir le résultat ces 32,2 nm ou -32,2 Nm[vert][/vert]

C'est -32.2 Nm, étant donné que la rotation se fait dans le sens antitrigonométrique (ou horaire)

D'accord merci mais du coup 150*0,2144 = a 32,2 Nm donc je comprend pas comment on peut trouver -32,2

Car il faut faire -150, le poids étant orienté vers le bas (sens opposé à l'axe y)

d * -||F|| = 0.2144 * -150 = -32.2

Par convention souvent utilisée : -32,2 Nm (puisque tend à tourner dans le sens horlogique).

Cependant, on peut parfaitement utiliser une convention différente ... mais souvent alors, on indique le sens positif à considérer sur le dessin.

Piqué sur wiki :

Mais est ce que ça veux dire que la norme du vecteur F est égale à 4,6m ?
ça me parait beaucoup