Inscription / Connexion Nouveau Sujet
Mécanique: Jet d'une pierre
Bonjour,
Qui peut me venir en aide pour résoudre cette exercice:
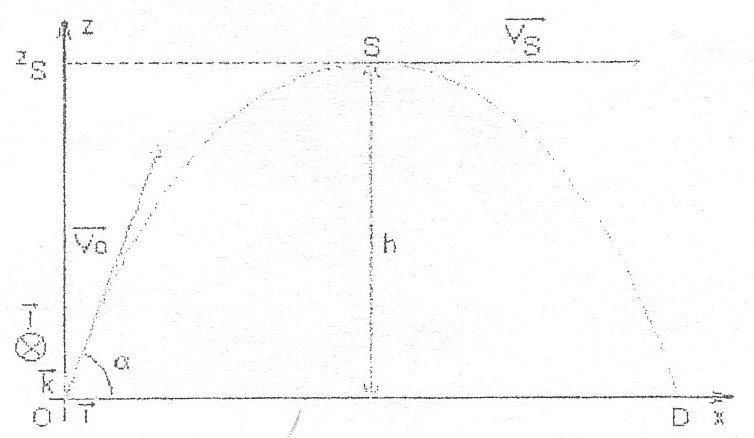
On lance d'un point O, une pierre de masse m= 100g avec un vecteur 
0 incliné d'un angle 
par rapport au plan horizontale, avec Vo= 15.0 m.s-1. La pierre décrit une trajectoire parabolique de sommet S.
Le point O est pris comme origine des altitudes et l'action de l'air est supposée négligeable.
1)a) Calculer les coordonnées Vox et Voy du vecteur vitesse initiale 0
--> Vox = cos * Vo
Voy= sin * Vo
C'est bon? Dois-je justifier, si oui comment?
b)Exprimer Vo en fonction de Vox et Voy
2) La vitesse au sommet de la trajectoire est horizontale et a pour valeur Vs = Vox
Déterminer l'expression littérale donnant l'altitude Zs du sommet S en fonction de Vox et
--> J'ai trouvé Vs = Vo * cos
3) Calculer Zs pour = 30,0° et =60,0°
4) Déterminer la vitesse de la pierre lorsqu'elle passe par le point D juste avant l'impact sur le sol
Merci d'avance à tous!
Bonjour,
Oui pour 1a
Et 1b ?
Non pour 2 ; tu as recopié Vs = Vox mais ce n'est pas ce qui est demandé ; on demande Zs
pour 1b) je ne vois pas comment exprimet Vo avec les cos et les sin...
ensuite comment exprimer Zs avec cos * VO et
???
Pour 1b :
V0 en fonction de V0x et V0y, c'est tout simplement le théorème de Pythagore.
Expression de Zs : elle sera plus facile en fonction de V0, de sin() et de g (pense à l'autre problème que tu as posté ; même raisonnement)
pour 1)b
donc avec Phytagore ca donne:
Vo² = Vox² + Voy²
Vo² = (cos * Vo)² + (sin * Vo)²
Vo = 
(cos * Vo) + (sin * Vo)
C'est ca?? Ce me semble un peu complexe...
pour ce qui est de l'expression de Zs faut faire intervenir l'Epp ? mais le je vois pa trop comment...
La racine carrée d'une somme n'est pas égale à la somme des racines carrées...
Au sommet de la parabole, le vecteur-vitesse est horizontal (vs = v0x)
La composante du vecteur-vitesse selon l'axe vertical est donc nulle.
La diminution correspondante de l'énergie cinétique correspond à l'augmentation d'énergie potentielle du système Terre-pierre en ce point de la trajectoire.
Ok pour la 1b)
Pour la 2)
Zs = (Vo + v0x)
(mais ca doit pas etre ca puisque il n'y pas alpha...)
Impossible... la racine carrée d'une vitesse ne peut pas être une longueur !
Quelle est la variation d'énergie potentielle du système Terre-pierre entre le point O et le point S de hauteur zS ?
Quelle est la variation d'énergie cinétique entre ces deux points sachant que
. en O la vitesse v0 est telle que v02 = v0x2 + v0y2
. et qu'en S la vitesse est telle que vS2 = v0x2
L'énergie mécanique se conservant en l'absence de frottements, quelle est en conséquence la hauteur zS ?
3)
C'est un peu comique de noter z l'axe vertical du repère pour la trajectoire et puis de noter vy pour la composante verticale de la vitesse.
Je continue dans cette voie, mais cela mériterait d'être remis sur ses pieds.
vy = Voy - gt
au sommet de la tajectoire, vy = 0 --> t = voy/g = Vo*sin(alpha) / g
y = Voy*t - gt²/2
y est max pour t = Vo*sin(alpha) / g
y max = Vo*sin(alpha)*Vo*sin(alpha) / g - g*Vo²*sin²(alpha) / 2g²
y max = (1/(2g)) Vo² * sin²(alpha)
zs = (1/(2g)) Vo² * sin²(alpha)
-----
Autrement.
Composante verticale de l'énergie cinétique au lancer = (1/2).m.(Voy)² = (1/2).m.Vo².cos²(alpha)
Cette énergie sera totalement transformée (en l'absence de frottement) en énergie potentielle au sommet de la trajectoire -->
(1/2).m.Vo².cos²(alpha) = mg.Zs
zs = (1/(2g)) Vo² * sin²(alpha)
-----
Sauf distraction.
Merci!
Juste une question pourquoi dis tu que l'énergie potentiel est égale a l'énergie cinétique au sommet de la trajectoire?
(1/2).m.Vo².cos²(alpha) = mg.Zs
zs = (1/(2g)) Vo² * sin²(alpha)
Pourquoi le cos se transforme en sin?
Pour le cos² en sin², il s'agit d'une erreur de copier coller.
-----
Energie mécanique = Energie cinétique + Energie potentielle
Et en l'absence de frottement, l'énergie mécanique se conserve pendant le mouvement.
Au lancer:
Energie cinétique = (1/2) m [(Vx)²+ (Vy)²]
Energie potentielle := 0 (puisque au rs du sol)
--> Energie mécanique = (1/2) m [(Vx)²+ (Vy)²]
Au sommet de la trajectoire.
Vx est le même qu'au départ mais Vy est nul -->
Energie cinétique = (1/2) m (Vx)²
Energie potentielle = mg.Zs
---> Energie mécanique = (1/2) m (Vx)² + mg.Zs
Comme il y a conservation de l'énergie macanique pendant le mouvement, on a:
(1/2) m [(Vx)²+ (Vy)²] = (1/2) m (Vx)² + mg.Zs
Soit en simplifiant:
(1/2) m (Vy)² = mg.Zs
(1/2).m.Vo².sin²(alpha) = mg.Zs
zs = (1/(2g)) Vo² * sin²(alpha)
-----
Pourquoi au sommet de la trajectoire Vy est nul ?
Si je calcule Zs avec alpha = 30°
Zs = 1/2*9.8*15²*sin(30)² = 275,625m
Ca faut un peu beaucoup non??
Ca ne serait pas plutot
Zs = ((1/2) x Vo2 x sin(alpha)) / g
2 = puissance de 2
Ne pas confondre (1/2)g avec 1/(2g).
zs = (1/(2g)) Vo² * sin²(alpha)
zs = (1/(2*9,81)) 15² * sin²(30°) = 5,73 m
dans la question il demande aussi fonction de Vox, comment le faire intervenir??
Mais ne peut t'on pas le retrouver avant la simplification?? puisqu'il y est present
zs = (1/(2*9,81)) 15² * sin²(30°) = 5,73 m
Quand je refais a la calculette ca me fait 2;86m??
Voila en reprenant et en essayant de faire apparaitre Vox je trouve:
(1/2) m [(Vx)²+ (Vy)²] = (1/2) m (Vx)² + mg.Zs
(1/2) m (Vox/cos)² = (1/2) m (Vx)² + mg.Zs
(1/2)(Vox/cos)² = (1/2) (Vx)² + mg.Zs
Zs = (1/(2*g))*(Vox/cos)²-(Vox)²
mais quand je calcul je trouve pas...
Bonjour à tous les deux,
Flash >
Tu as raison pour ZS (dans le cas où = 30°) c'est bien 
2,87 m
Ton calcul de 21 h 49 est faux
Je repars de la première ligne :
(1/2) m [(Vx)2+ (Vy)2] = (1/2) m (Vx)2 + mg.Zs
(1/2) m Vx2 + (1/2) m Vy2 = (1/2) m Vx2 + m.g.ZS
(1/2) m Vy2 = m g ZS
Annuler
connectez vous