Inscription / Connexion Nouveau Sujet
Loi de Kirchoff
Bonjour ,
Serait il possible de m'aider a propos de cet exercice , j' ai essayer de calculer la reistsance equivalente au debut de facon simple et je trouve 3R/5 , avec le theoreme de kennely et je trouve que cela vaut 5R , j'ai rajouté des fleches d'intensité en bas du circuit mais je ne suis pas sur que cela est vrai.
Voici les questions
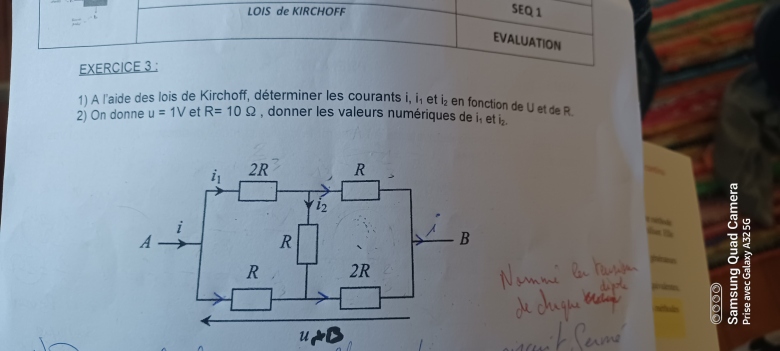
1) A l aide des lois de kirchoff , determiner les courants i, i1 et i2 en fonction de U et de R
2)On donne u=1V et R=10 ohm , donner les valeurs numeriques de i1 et i2
Merci de votre aide
J'envoie le cricuit dans quelque minute
Bonjour
C'est vrai que le théorème de Kennely permettrait d'obtenir la résistance équivalente entre A et B et donc d'obtenir l'expression de i. Cependant, l'énoncé demande d'utiliser exclusivement la loi des nœuds et des mailles.
Tu pourrais commencer, directement sur le schéma, par indiquer les intensités des courants à travers toutes les résistances du circuit en utilisant la loi des nœuds. Ensuite la loi des mailles permet d'obtenir le résultat.
Merci beaucoup , il n y a donc pas besoin de calculer la resistance equivalente ?
Je voulais egalement savoir si il y a une intensité qui part du bas vers la branche centrale et donc vers i2 , si c est le cas ,le courant et donc la resistance serait egal a 0 ?
Commencer par calculer la résistance équivalente est une méthode correcte mais cela ne semble pas être celle demandée ici.
Avant de te lancer dans l'utilisation de la loi des mailles et afin de ne pas multiplier le nombre d'inconnues, tu peux remarquer que la loi des nœuds conduit à :
intensité à travers R en haut à droite : (i1-i2)
intensité à travers R en bas à gauche : (i-i1)
intensité à travers 2R en bas à droite : (i-i1+i2)
PS : au fait : la résistance équivalente, vue des bornes A et B, ne vaut ni 5R ni 3R/5. Tu as dû te tromper dans l'utilisation du théorème de Kennely mais cela importe peu puisque la méthode demandée n'utilise pas ce résultat...
Mince ! Je pense que j'ai du mal appliquer le theoreme , pour le 3R/5 c'etait une des valeurs que j'avais trouvé mais je doutais bien que ce n etait pas cela , je ne voyais pas trop comment calculer la resistance equivalente sans le theoreme de kennely dans ce circuit.
Je vous remercie a nouveau pour l'aide , je trouve que Uab=2Ri1 + R(i1-i2) , je ne suis pas sur que j'ai bien utiliser la loi des mailles mais je trouve que R(i-i1)=Ri2+2Ri et Ri2=2R(i-i1+i2)+ R(i1-i2) , faudrait il utiliser le diviseur de tension pour trouver les tensions ?
Je viens de voir que la tension central est egal a la tension en haut a droite - la tension en bas a droite (car elle est opposé ducoup +(-))
D'où tires-tu cela ?
Une méthode possible et assez rapide consiste à appliquer la loi des maille à la petite maille de droite puis à la petite maille de gauche. Cela même simplement aux égalités :
i=3i1+i2 ;
i1=-2i2 ;
Exprimer la tension U comme la somme des tensions aux bornes des deux résistances horizontales du bas conduit, en tenant compte des relations précédentes, à une expression de i en fonction de U/R.
On peut éventuellement montrer (cela n'est pas demandé par l'énoncé) que le résultat est cohérent avec l'expression de la résistance équivalente du circuit déduite du théorème de Kennely :
On a effectivement i2<0 mais je n'obtiens pas ton expression. Es-tu arrivé à démontrer les deux égalités entre intensités de mon message précédent ?
Ensuite, considérer U comme la somme des tensions aux bornes deux deux résistances horizontales du bas ou du haut conduit à :
Compte tenu des deux relations que j'ai déjà fournies, on peut exprimer i1, i2 et i en fonction de (U/R).
Excusez moi je m'etais trompé , je trouve donc , en injectant i1=-i2 dans la relation i2=-u/7R et i1=2U/7R (comme i1=-2i)
Pour les egalités je ne comprend pas bien comment vous arrivez a trouver ce resultat , prenons la maille de droite fait vous la ressistance central = resistance bas droite + reistsance haut droite?
i2=-U/7R et i1=2U/7R
D'accord avec toi malgré ton étourderie de copie d'une des formules fournies à 18h11.
Pour l'égalité fournie à 19h02, je n'utilise pas la loi des mailles mais simplement l'addition des tensions : la tension U est la somme de la tension aux bornes de la résistance 2R en haut à gauche et de la tension aux bornes de la résistance en haut à droite :
Petite maille de gauche après division de tous les termes par R :
Petite maille de droite après division de tous les termes par R :
C'est immédiat si, comme conseillé à 16h25, tu as bien précisé sur le schéma les expressions des intensités de courants à travers toutes les résistances, ces expressions faisant intervenir i, i1 et i2.