Inscription / Connexion Nouveau Sujet
Les mouvements
Bonjour à tous
Voici un autre exo que j'arrive pas donc s'il vous plait une petite aide sera pas de refus
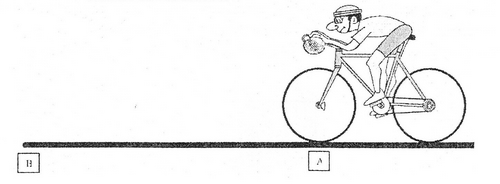
Un cycliste se déplace sur une piste horizontale à vitesse contante de A à B.
A la verticale du point A, il lache une balle et continue sa course vers le point B.
Réprésentez sur le schéma ci-dessous la manière dont vous voyez tomber la balle et indiquez l'endroit ou, selon vous, se trouvera le cycliste et son velo lorques la balle touchera le sol
Remarque : La réponse doit être précise et argumentée.
Quelle expérience peut-on concevoir afin de vérifier ou d'invalider cette hypothèse ? merci d'avance de votre aide
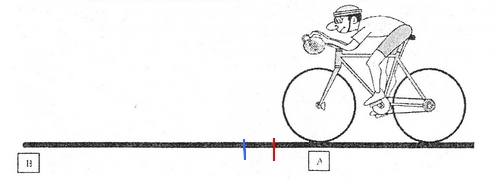
Le rouge c'est ou la salle touchera le sol et le bleu c'est ou le cycliste sera mais il y aura très peu de différence car le balle va très vite touchait le sol mais comment l'expliquer et l'argumenter la je bloque
Bonsoir,
C'est un problème de référentiel...
Dans le référentiel du vélo (qui est galiléen...le référentiel, pas le vélo ...), la balle est en chute libre donc elle tombe à la verticale.
...), la balle est en chute libre donc elle tombe à la verticale.
Si la durée de la chute est T secondes, le vélo va se déplacer de vT mètres (v étant la vitesse du vélo). Et c'est l'endroit où la balle va toucher le sol.
Si on se place dans un référentiel lié à la route, la balle se déplace horizontalement à la vitesse (vitesse du vélo) avant d'être lâchée.
Quand elle est lâchée, elle est soumise à une seule force verticale, son poids, et elle a une vitesse initiale égale à (vitesse du vélo). Elle décrit donc une parabole
... et elle tombera au même point que celui trouvé dans le référentiel du vélo...
"Quelle expérience peut-on concevoir afin de vérifier ou d'invalider cette hypothèse ?"...
Je pense qu'on peut faire l'expérience suivante :
Sans le vélo, à la verticale du point A et à la même hauteur, on lance la balle avec une vitesse égale à la vitesse du vélo. Elle doit tomber au même endroit qu'avec le vélo...
Oups ! L'équation de la parabole est fausse...
en fonction du temps
ou
avec l'axe y perpendiculaire à la route orienté vers le haut et l'axe x parallèle à la route orienté dans le sens d'avancement du vélo...
Voilà ce "petit" problème réparé  ...
...
Il est très important de bien comprendre ce genre d'exo...
Cela ne te paraît peut-être pas important mais je t'assure que ça l'est...
Pour être plus précis, si l'origine du repère est en A et l'axe y perpendiculaire à la route orienté vers le haut et l'axe x parallèle à la route orienté dans le sens d'avancement du vélo, l'équation de la parabole est :
ou
h étant la hauteur de laquelle on lâche la balle...
Pour trouver le x auquel la balle touche le sol, il suffit de faire y = 0 ==>
De la même façon, on peut trouver le temps...
Cette précision était nécessaire  ...
...


