Inscription / Connexion Nouveau Sujet
Les 3 nageurs
Pour ce sujet je ne comprend rien trois nageur A B C plongent au même instant dans une rivière dont le courant a une vitesse u= 0,5m/s par rapport au rive. A suit le courant, B remonte le courant et C nage perpendiculairement a la rive. Chaque nageur a par rapport a l'eau une vitesse v=0,75m/s. 1/ quelle est la vitesse de chaque nageur par rapport aux rives? 2/ au bout de 60s qu'elle distance a parcourue chaque nageur par rapport aux rives merci pour la reponses
Bonjour,
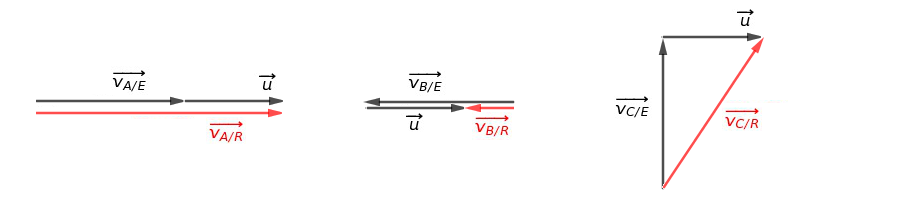
Pour le nageur A :
Autrement dit :
Le vecteur vitesse de A par rapport à la rive est égal à la somme des vecteurs vitesses de A par rapport à l'eau et de l'eau par rapport à la rive.
En projetant cette relation vectorielle sur un axe orienté et parallèle à la rive on trouve la norme du vecteur vitesse de A par rapport à la rive.
Je te laisse le soin d'étudier les cas des nageurs B et C
Pour C ( Comme pour A ou pour B )
Tu sais probablement additionner des vecteurs ...
Le résultat peut s'obtenir comme précédemment par projection de la relation vectorielle ci-dessus sur un axe orienté et parallèle à la rive ou bien en appliquant le théorème de Pythagore.